该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

靶场

题目背景

tiger是远近$\tiny\text{不}$闻名的射击$\tiny\text{游戏}$高手，十分擅长射击。 一天有一个叫做$\color{white}你不会知道$的人找到他，而他非常有责任心的抱去靶场打靶子了。

题目描述

靶场可以抽象为 $2$ 个平台和 $1$ 个障碍物。

你将会在样例解释中见到图片。 现在tiger站在平台A上且可以在平台A内随意移动，而在平台B的每个整点上各有一个靶子。 tiger的手中有一把射程无限的玩具枪，子弹的路径是一条直线。

• 简单来说，当tiger的位置和靶子所形成的直线不经过障碍物时，tiger可以击中靶子。

现在《勤学好问》的tiger想问问你他最多可以击中多少个靶子。

输入格式

第一行一个正整数 $T$，代表数据组数。 接下来 $T$ 行，每行六个整数 $a,b,c,d,e,f$，含义如题。

输出格式

输出 $T$ 行，每行一个整数代表这组数据的答案，对 $10^9+7$ 取模。

样例 #1

样例输入 #1

3
4 3 3 2 2 3
6 4 2 1 5 4
9 8 1 7 8 1

样例输出 #1

8
5
1

提示

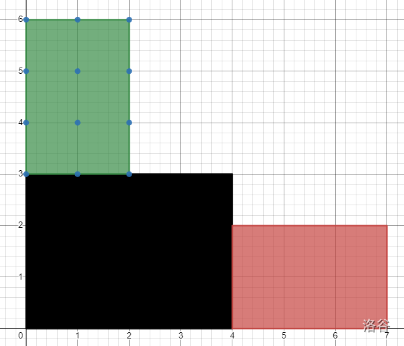
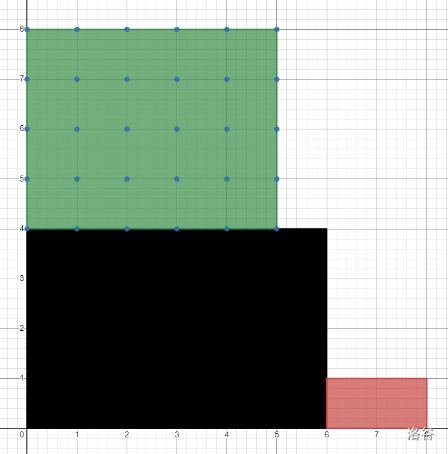分别有 $8$ 个和 $5$ 个靶子可以被击中。

数据范围

对于 $100\%$ 的数据：

• $a,b,c,d,e,f$ 为正整数。
• $d<b,e<a$。
• $1\leq T\leq50$，E1部分除外。
• 每部分数据将分别储存在subtasks中，但是不开启捆绑测试。

注意本题不存在 $1\leq a,b,c,d,e,f\leq 10^{9}$ 的极限数据。