21 Days Training // Day 19

T2. binary

My idea : still enum.

Enumerate all possible substrings and check.

Quick check :

Notice that 2^{2n+1} \equiv 1 \pmod{3} and 2^{2n} \equiv -1 \pmod{3}

So we can get under conclusions :

1. If the string is full of 0, it is valid.
2. If the string has only 1 position that is 1, it is invalid.
3. If the string has even number of 1s, it is valid, since we can put these 1s on 2^0, 2^1, 2^2, etc. According to the conclusion above, the remainder of the string is 0.
4. If the string has odd number of 1s and it has no more than one 0, it is invalid, otherwise, it is valid. Since we can get 3 of 1s and put hem as 10101, and the remain puts as above. According to the conclusion above, the remainder of the string is also 0. However, to achieve this, we need at least 2 zeros. If there is only 1 zero or no zeros, we cannot move as this.

Therefore, for a string, follow the steps above, you can know if it is valid.

Code :

#include <bits/stdc++.h>
using namespace std;

int main() {
    int N;cin >> N;
    int A[N];
    for (int i=0;i<N;i++) cin >> A[i];
    int Q;cin >> Q;
    for (int i=0;i<Q;i++) {
        int opt;cin >> opt;
        if (opt==1) {
            int t;cin >> t;t--;
            A[t] = 1-A[t];
        }
        else {
            int l, r;cin >> l >> r;l--;r--;
            long long ans=0;
            for (int lx=l;lx<=r;lx++) {
                for (int rx=lx;rx<=r;rx++) {
                    if (lx==rx) {
                        ans += (1-A[lx]);
                    }
                    else {
                        int c1=0;
                        for (int p=lx;p<=rx;p++) c1 += A[p];
                        if (c1==1) continue;
                        if (!(c1&1)) ans++;
                        else if ((rx-lx+1-c1)>=2) ans++;
                    }
                }
            }
            cout << ans << endl;
        }
    }
    return 0;
}

Constraints :

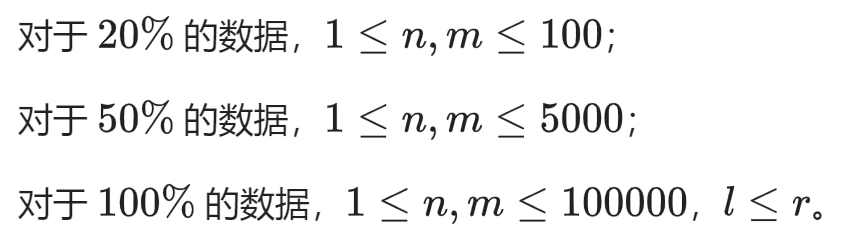
Expected : 0/20

(I forgot the judge of condition 2.)