GDNOJ – DAY 17 – 1

Posted on By 张, 高畅 GDNOJ – DAY 17 – 1无评论

理论上我们不应该这么早就开始动 blog。

但是这只是理论上。

Baby watchin’ it burn, send death to isolation
Oh watchin’ it burn, ain’t got no hesitation
Watchin’ it burn, we’re fallin’ higher
— HOYO-MIX/YMIR,耀斑

[A]

二维DP，但是最开始硬是一维乱搞搞不出来。

设 $f{i, j}表示第一条路径最后点为i，第二条路经最后点为j，设k = \max(i,j) + 1，有转移：f{k, j} = f{i, j} + dis{i, k}和f{i, k} = f{i, j} + dis_{j, k}$ 。

注意特判 i = p_1 和 j = p_2 的情况，不能转移。

#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<double, double> PDD;
const int N = 1005;
const double INF = 1e9;
double f[N][N], dist[N][N];
int n, p1, p2;
PDD w[N];
double get(PDD a, PDD b){return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));}
int main()
{
    freopen("path.in", "r", stdin);
    freopen("path.out", "w", stdout);
    scanf("%d%d%d", &n, &p1, &p2);
    p1 ++, p2 ++; 
    for (int i = 1; i <= n; i ++)scanf("%lf%lf", &w[i].x, &w[i].y);
    for (int i = 1; i <= n; i ++)
    {
        for (int j = 1; j <= n; j ++)
        {
            if (i != j)dist[i][j] = get(w[i], w[j]);
            f[i][j] = INF;
        }
    }
    f[1][1] = 0;
    for (int i = 1; i < n; i ++)
    {
        for (int j = 1; j < n; j ++)
        {
            if (i != 1 && j != 1 && i == j)continue;
            if (i == p2 || j == p1)continue;
            int k = max(i, j) + 1;
            if (k != p1)f[i][k] = min(f[i][k], f[i][j] + dist[j][k]);
            if (k != p2)f[k][j] = min(f[k][j], f[i][j] + dist[i][k]);
        }
    }
    for (int i = p1; i < n; i ++)f[n][n] = min(f[n][n], f[i][n] + dist[i][n]);
    for (int i = p2; i < n; i ++)f[n][n] = min(f[n][n], f[n][i] + dist[i][n]);
    printf("%.2lf", f[n][n]);
    return 0;
}

[B]

第二题就放紫，真的好吗。

首先这个问题的答案就是最小路径覆盖，证明不会，直观上直接选路径覆盖的首端一定是合法的。

最小路径覆盖可以考虑先用 n 条路径覆盖所有点，然后类并查集似的合并，因此直接用总点数 – 最大流就是答案。

有二分图性质，可以直接 KM O(nm) （实际远小于这个数）跑二分图匹配。

#include<bits/stdc++.h>
using namespace std;
const int N = 205;
int n, m, match[N], st[N];
int g[N][N];
bool find(int u)
{
    for (int i = 1; i <= n; i ++)
    {
        if (g[u][i] && !st[i])
        {
            st[i] = 1;
            if (!match[i] || find(match[i]))
            {
                match[i] = u;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    scanf("%d%d", &n, &m);
    while (m --)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        g[a][b] = 1;
    }
    for (int k = 1; k <= n; k ++)
    {
        for (int i = 1; i <= n; i ++)
        {
            for (int j = 1; j <= n; j ++)g[i][j] |= g[i][k] & g[k][j];
        }
    }
    int res = 0;
    for (int i = 1; i <= n; i ++)
    {
        memset(st, 0, sizeof st);
        res += find(i);
    }
    printf("%d\n", n - res); 
    return 0;
}

[C]

网上题解大部分都是错的，建议网上题解和官解打一架。

首先既然是对称，不难想到回文。再加上是环，因此破环成链，把原数组复制一遍，跑 manacher。

跑完后，我们考虑什么情况下满足拼起来合法情况。

设两个回文中心为 i 和 j， p_i 表示回文半径（注意就是大部分 manacher 跑出来要减 1），那么有：

  • $ j – i \leq n$
  • $i + p_i \geq j – p_j$（是的大部分网上题解这一条写的是错的）

可能比较难以理解，放一个图。

上面部分代表第一条，下面部分代表第二条为什么符号是这样的。

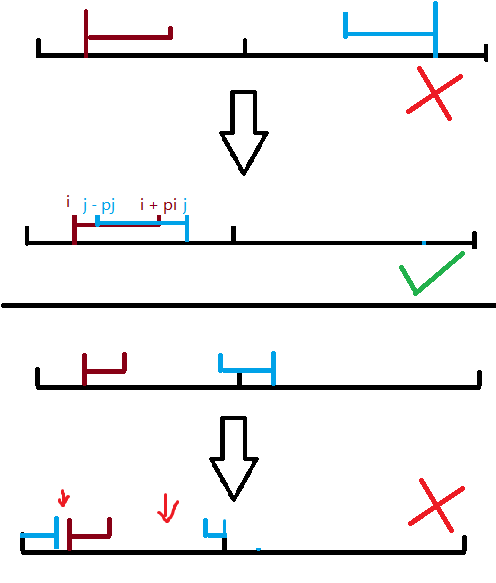
可能更难理解了

这个东西很显然的，用线段树维护，官解还有扫描线+并查集的超优做法，不学了。

注意因为 i – p_i 很有可能是 0，（我的）线段树会死机，因此在实现中我进行了 +1 的处理，代码注释也有解释这一点。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m, res, p[N << 2], tr[N << 4];
char a[N << 1], s[N << 2];
void init()
{
    int k = 0;
    s[k ++] = &#039;$&#039;;
    s[k ++] = &#039;#&#039;;
    for(int i = 0; i < n; i ++)
    {
        s[k ++] = a[i];
        s[k ++] = &#039;#&#039;;
    }
    s[k ++] = &#039;^&#039;;
    m = k;
}
void manacher()
{
    int mr = 0, mid = 0;
    for(int i = 1; i < m; i ++)
    {
        if (i < mr)p[i] = min(p[mid * 2 - i], mr - i);
        else p[i] = 1;
        while (s[i - p[i]] == s[i + p[i]])p[i] ++;
        if(i + p[i] > mr)
        {
            mr = i + p[i];
            mid = i;
        }
    }
}
void pushup(int u){tr[u] = max(tr[u << 1], tr[u << 1 | 1]);}
void modify(int u, int l, int r, int pos, int v)
{
    if (l == r)
    {
        tr[u] = v;
        return;
    }
    int mid = l + r >> 1;
    if (pos <= mid)modify(u << 1, l, mid, pos, v);
    else modify(u << 1 | 1, mid + 1, r, pos, v);
    pushup(u);
}
int query(int u, int l, int r, int L, int R)
{
    if (L <= l && r <= R)return tr[u];
    int mid = l + r >> 1;
    int res = 0;
    if (L <= mid)res = max(res, query(u << 1, l, mid, L, R));
    if (mid < R)res = max(res, query(u << 1 | 1, mid + 1, r, L, R));
    return res;
}
int main()
{
    scanf("%s", a);
    n = strlen(a);
    for (int i = 0; i < n; i ++)a[n + i] = a[i];
    n = (n << 1);
    init(), manacher();
    for (int i = 0; i < m; i ++)p[i] --; //[i - p[i] , i + p[i]] 回文
    n >>= 1; 
    //j - 1 <= n
    //attention : actually we find i + p[i] + 1 >= j - p[j] + 1 rather than i + p[i] >= j - p[j]
    for (int i = 1; i <= n + 1; i ++)modify(1, 1, m, i - p[i] + 1, i);
    for (int i = 1; n + i + 1 < m; i ++)
    {
        if (query(1, 1, m, i - p[i] + 1, i - p[i] + 1) == i)modify(1, 1, m, i - p[i] + 1, 0);
        res = max(res, query(1, 1, m, 1, i + p[i] + 1) - i);    
        modify(1, 1, m, (n + i + 1) - p[n + i + 1] + 1, n + i + 1);
    }
    printf("%d", res);
    return 0;
}

吃过晚饭再来另开一个（主要是剩下的不是很可改

训练日志

发表回复