早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
学算法
1. 动态 DP
模板题
题解
广义矩阵乘法
定义广义矩阵乘法 A \times B=C 为: C_{i,j}=\max\limits_{k=1}\limits^{n}{A_{i,k}+B_{k,j}}
相当于将普通的矩阵乘法中的乘变为加,加变为 \max 操作。
同时广义矩阵乘法满足结合律,所以可以使用矩阵快速幂。
不带修改操作
令 dp_{i,0} 表示不选择 i 的最大答案,dp_{i,1} 表示选择 i 的最大答案。
则有 DP 方程: dp_{i,0}=\sum\limits_{son}{max(dp_{son,0},dp_{son,1})}
dp_{i,1}=w_i+\sum\limits_{son}{dp_{son,0}}
答案就是 \max(f_{root,0},f_{root,1}).
带修改操作
首先将这棵树进行树链剖分,假设有这样一条重链:
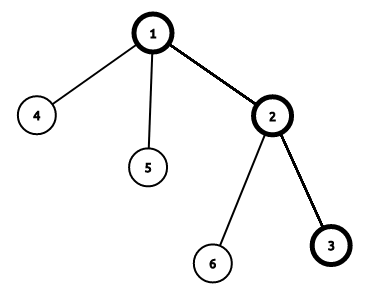
设 g_{i,0} 表示不选择 i 且只允许选择 i 的轻儿子所在子树的最大答案,g_{i,1} 表示不考虑 son_i 的情况下选择 i 的最大答案,son_i 表示 i 的重儿子。
假设我们已知 g_{i,0/1} 那么有 DP 方程: dp_{i,0}=g_{i,0}+max(dp_{son_i,0},dp_{son_i,1})
dp_{i,1}=g_{i,1}+dp_{son_i,0}
答案是 \max(f_{root,0},f_{root,1}).
可以构造出矩阵: \begin{bmatrix}g_{i,0}&g_{i,0} \\ g_{i,1}&-\infty \end{bmatrix} \times \begin{bmatrix} dp_{son_i,0} \\ dp_{son_i,1} \end{bmatrix} = \begin{bmatrix} dp_{i,0} \\ dp_{i,1} \end{bmatrix}
注意,我们这里使用的是广义乘法规则。
可以发现,修改操作时只需要修改 g_{i,1} 和每条往上的重链即可。
具体思路
- DFS 预处理求出 f_{i,0/1} 和 g_{i,0/1}.
- 对这棵树进行树链剖分(注意,因为我们对一个点进行询问需要计算从该点到该点所在的重链末尾的区间矩阵乘,所以对于每一个点记录 End_i 表示 i 所在的重链末尾节点编号),每一条重链建立线段树,线段树维护 g 矩阵和 g 矩阵区间乘积。
- 修改时首先修改 g_{i,1} 和线段树中 i 节点的矩阵,计算 top_i 矩阵的变化量,修改到 fa_{top_i} 矩阵。
- 查询时就是 1 到其所在的重链末尾的区间乘,最后取一个 \max 即可。
代码实现