21 Days Training // Day 13

T0. math

My idea :

Let f(n)=x^n+x^{-n} . Notice that f(1)=k
And when 2 \mid n , f^2(\frac{n}{2}) = (x^{\frac{n}{2}}+x^{-\frac{n}{2}})^2=x^n+x^{-n}+2x^{\frac{n}{2}}x^{-\frac{n}{2}} = f(n)+2 .
Therefore, 2 \mid n , f(n) = f^2(\frac{n}{2})-2 .

Based on this formula, we can get f(n) withb a complexity of O(\log_2 n) .

Bug :

When 2 \nmid n , f^2(\frac{n-1}{2}) = f(n-1)-2 .
Now we need to solve f(n-1) .

But, currently, I found this formula : f(n-1)f(1) = (x^{n-1}+x^{-n+1})(x+x^{-1}) = x^n + x^{-n} + x^{n-2} + x^{-n+2} = f(n) + f(n-2) .

Therefore, f(n) = f(n-1)f(1)-f(n-2) .
If we directly use above idea to solve it, the complexity will be O(n) , TLE.

(Right) idea :

Actually, we are colse enough to the answer.
Notice that f(1) is a given constant k .
So the equation will be f(n) = kf(n-1)-f(n-2) .
Seems familiar?
When we meet such formula… we can use matrix!

T0-EX. Matrix qkp Extension

Did you still remember this passage ?
There, we show the example of solving fibonacci numbers with matrix.
In fact, it can be used in such problems.

Thing about the form of the matrix :

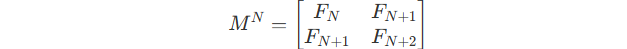
And how we get M^{N+1} :

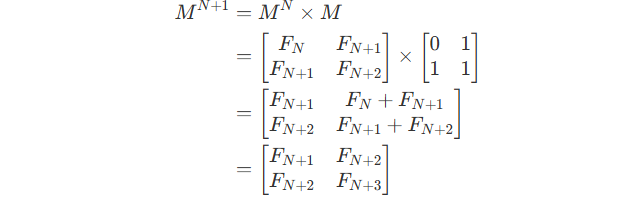
Here, we designed a matrix M so that it satisfies those properties above.

However, the generalize this method, we face 2 problems :

1. Sometimes the initial condition not equals to M.
2. Sometimes the coefficient changes, maybe (2, 3), (5, 8), (114514, 191981).

For the first problem, just change the formula : M^N into M_0 \times M^N .

Here, M_0 is the initial status of the sequence, M shows the relations between these terms in the sequence.

For the second problem, go back to the equation.

Suppose that we have a sequence that satisfies $AN = pA{N-1} + qA_{N-2}$ .

And we have calculated

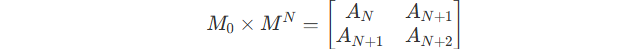
Now we expected to get M_0 \times M^{N+1} by calculating :

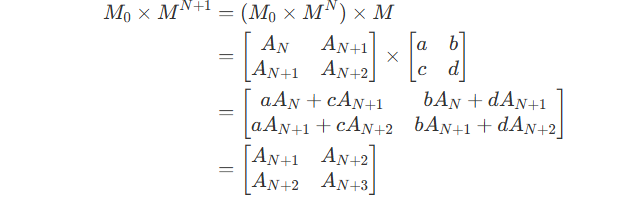
By comparing the terms, we can get :

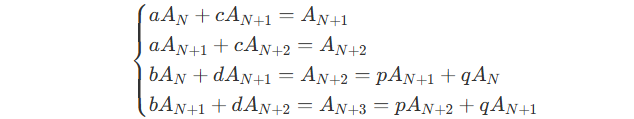
By comparing the coefficients, we can get :

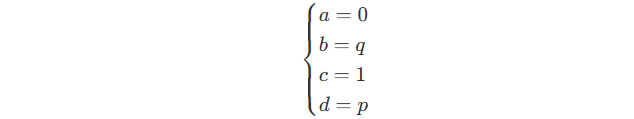
So the matrix M is :

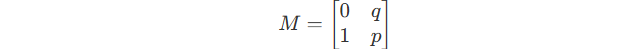
To initialize, the matrix M_0 should be :

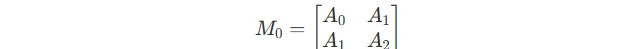
So, based on M_0 and M , we can solve the sequence quickly!

T0. math (Part II)

If you read the prev. page carefully, you must know how to use the conclusion.

Go back to the formula f(n) = kf(n-1)-f(n-2) .
If we consider f(n) as an element of a sequence, just set p=k, q=-1 , we can solve f(n) by matrix qkp.

Code :

#include <bits/stdc++.h>
using namespace std;
typedef vector<long long> V1D;
typedef vector<V1D> V2D;

class Matrix {
    private:
        V2D value;
        long long MH, MW;
    public :
        // Matrix() {}
        Matrix(V2D Vec) {value=Vec;MH=Vec.size(), MW=Vec[0].size();}
        Matrix(long long H, long long W) {
            MH=H, MW=W;
            for (long long i=0;i<H;i++) value.push_back(V1D(W));
        }
        long long getHeight() {return MH;}
        long long getWidth() {return MW;}
        long long getValue(long long y, long long x) {return value[y][x];}
        void change(long long y, long long x, long long v) {value[y][x] = v;}
        V2D matrixVec() {return value;}
        Matrix operator+(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (Hx != MH || Wx != MW) {
                cout << "Matrix Exception (operator+, E1) : Size not equal.";
                exit(0);
            }
            Matrix Mr(MH, MW);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<MW;j++) Mr.change(i, j, value[i][j]+Mx.getValue(i, j));
            }
            return Mr;
        }
        Matrix operator-(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (Hx != MH || Wx != MW) {
                cout << "Matrix Exception (operator-, E2) : Size not equal.";
                exit(0);
            }
            Matrix Mr(MH, MW);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<MW;j++) Mr.change(i, j, value[i][j]-Mx.getValue(i, j));
            }
            return Mr;
        }
        Matrix operator*(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (MW!=Hx) {
                cout << "Matrix Exception (operator*, E3) : Illegal H/W.";
                exit(0);
            }
            Matrix Mr(MH, Wx);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<Wx;j++) {
                    long long cur=0;
                    for (long long k=0;k<MW;k++) cur += value[i][k] * Mx.getValue(k, j);
                    Mr.change(i, j, cur);
                }
            }
            return Mr;
        }
        Matrix operator%(long long MOD) {
            Matrix Mr(value);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<MW;j++) Mr.change(i, j, Mr.getValue(i, j)%MOD);
            }
            return Mr;
        }
};

Matrix UnitMatrix(long long K) {
    Matrix M0(K, K);
    for (long long i=0;i<K;i++) M0.change(i, i, 1);
    return M0;
};

Matrix qkMpow(Matrix Mx, long long e, long long MOD) {
    long long K = Mx.getHeight();
    if (e==0) return UnitMatrix(K);
    if (e==1) return Mx;
    Matrix HF = qkMpow(Mx, e/2, MOD);
    if (e&1) return ((HF*HF)*Mx)%MOD;
    return (HF*HF)%MOD;
};

int main() {
    long long N, K, MD;cin >> MD >> K >> N;
    Matrix M0(2, 2), MP(2, 2);
    M0.change(0, 0, 2);
    M0.change(0, 1, K);
    M0.change(1, 0, K);
    M0.change(1, 1, ((K*K)%MD-2+MD)%MD);
    MP.change(0, 1, -1);
    MP.change(1, 0, 1);
    MP.change(1, 1, K);
    Matrix Mx = qkMpow(MP, N, MD);
    Matrix M = M0*Mx;
    V2D Vec = M.matrixVec();
    cout << (Vec[0][0]+MD)%MD;

    return 0;
}

Note :
Because the coefficient q is negative, when get the result, add it by MD and modulo it again.

This code can correctly answer all samples.
Not all cases!