早上自习
今天没比赛,自己复习一下Tarjan,试图搞懂原理,便于记忆
Tarjan 求强连通分量
模板题 Luogu B3609
之前在常州的时候为了方便,打的是Kosaraju算法(其实这个我也忘了)
但没事,我们今天主要学Tarjan
以下给出几个定义(后面也会用到)
首先,强连通分量是指在有向图中,其子图中各顶点两两连通,且包含的点尽可能的多
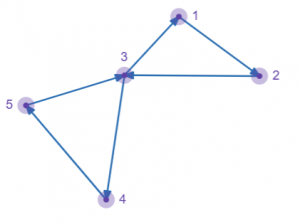
怎么理解后半句呢?比如上面这个图,虽然由(1,2,3)构成的环好像也符合两两连通的条件,但是在加入(4,5)后,构成的图(1,2,3,4,5)仍然符合两两连通,因此(1,2,3)就不是一个强连通分量,但(1,2,3,4,5)是
(特别地,孤立点也是强连通分量)
接下来是关于DFS的
首先是DFS生成树,是指将图经过DFS遍历后,遍历时真正经过的边形成的树
这样就可以把一个图中的边分成以下几种边:
1.树边:在DFS树上的边
2.回边(反祖边):由后代指向根节点的边
3.前向边:由祖先指向后代(非儿子)的边
4.以上三种边都不是的即横向边
接下来会用到的数组或变量的含义
dfs_clock:时间戳
dfn:访问节点的次序
T(u):以u为根节点的子树 特别地,记T为DFS生成树
low(u)=min(dfn(v),low(u)) v∈T(u)
初始化:dfn(u)=low(u)=dfs_clock
对于low(u)的更新:
我们发现可以递归地思考,有
low(u)=min(low(v),low(u)) v∈T(u)
但对于反祖边,我们需要特别处理
low(u)=min(dfn(v),low(u)) v∈T(u)
下面来自OI_WIKI

我们给出结论,当我们将访问过的节点用栈存储后,在回溯的过程中,若发现dfn(u)=low(u),则u至栈顶的顶点属于同一个强连通分量
证明如下:
若有强连通分量,则必然在搜索时会遇到回边,因此每次low数组更新时,总无法有dfn(u)=low(u),只有最开始被访问到的该强连通分量的节点保留dfn(u)=low(u)的关系
好了,我们可以自己实现代码了
人生第一次不看模板写出Tarjan算法模板

压行看着有点难受,凑合看吧,但理解原理后,确实打起来感觉简单不少
下午自习 割点与桥+双连通分量
以下图不分有向与无向,对于有向图连通的说法,指有向图强连通
割点+点双连通分量
概念:
割点:将该点删除后使得原连通图分裂为多个子图的点即割点
点双连通:不存在割点的连通图
点双连通分量:图中极大的点双连通子图(此处对于分量/极大的理解类比强连通分量)
对于割点的求法,判断是否有low(v)>=dfn(u),v∈T(u)若有,则u为割点
但是对于T的根节点root(后面简记为R),无法用此法判断,因此我们需要单独看,若R的在DFS树上的度数不为1,则R是割点
证明如下:
对于第一种情况,若low(v)>=dfn(u)说明v只与T(u)中的点有连边,若将u删去,则必然会同不在T(u)中的点断开联系,因此u是割点
对于情况二,若R在DFS树上的度大于1,显然R会是割点
Code:
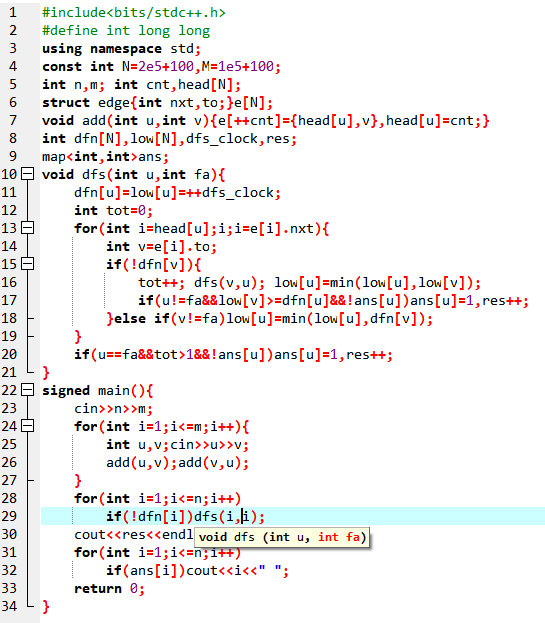
对于点双连通分量的求法,我们先看一下OI_WIKI给的一些性质

核心Code:
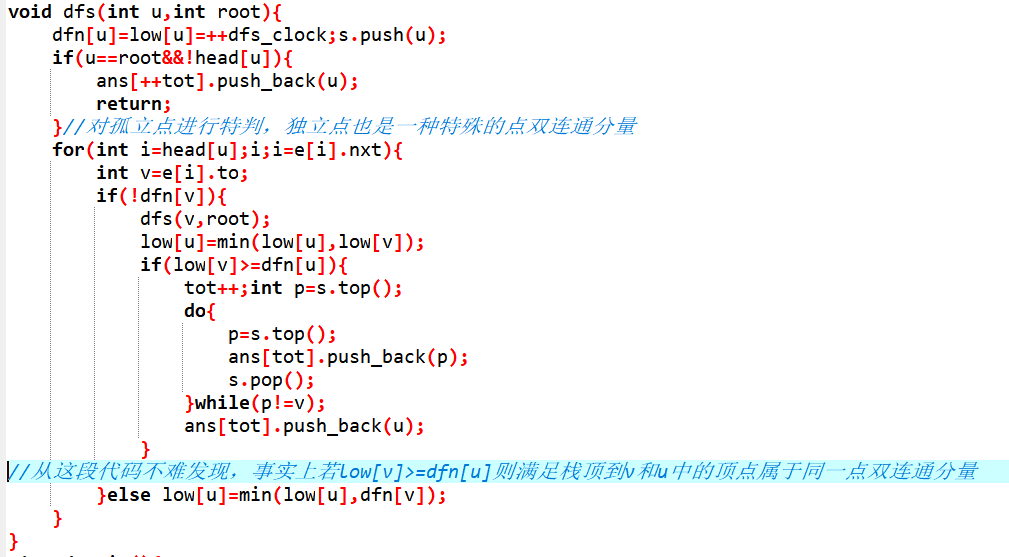
桥(割边)+边双连通分量
概念:
割边(桥):指将该边删去后使得原连通图分裂为多个子图的边
边双连通:不存在割边的连通图
边双连通分量:图中极大的边双连通子图
对于桥的求法

若有重边,无论哪条重边都不可能为桥,这种情况单独判断即可
模板题 Luogu P1656
以下是无重边求桥版的
Code:
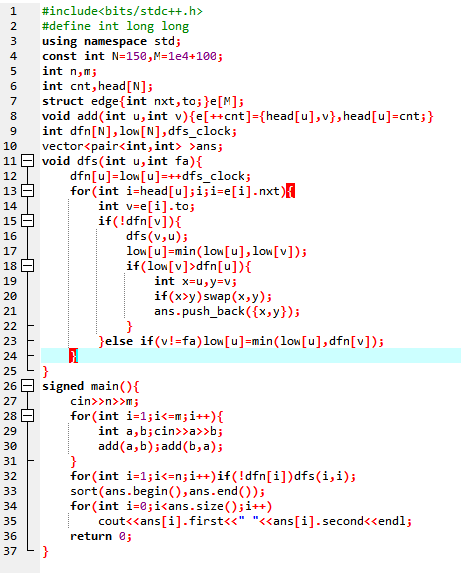
边双连通分量的求解:
我们可以根据定义求解,注意到边双连通分量中不存在桥,因此我们可以先将所有的桥求出,再用DFS求解边双连通分量
但是还有另一种思路

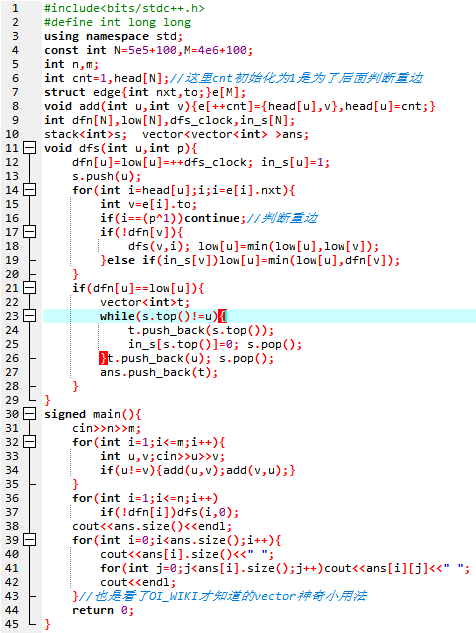
Tarjan小结
我认为Tarjan算法的核心思想是利用在图中遍历时dfn和low,根据如割点、割边等它们的一些性质,发现low与dfn之间的关系,利用这种关系进行判断是否为我们所要求的,我认为最重要的是对dfn和low的更新的记忆,以及这些概念的性质,判断方式的记忆
晚自习
不行了,Tarjan模板快打吐了🤮
看OI_WIKI了,博客就水到这里,拜拜