double我的一生之敌(因为浮点数和精度问题已经挂好几次了)
题目不想放了,看别人的Blog吧
T1
又差一点场切T1(小数点后少保留一位,100 \rightarrow 60),比较简单,考虑DP
我们设P_i表示连续选i个相同颜色的概率,
不难得到P_i = P_{i – 1} \times \frac{1}{m}
接下来假装有一个第0位,并假装他有颜色,我们设$dp{i,0/1}$表示第i个位置与第0位的颜色相同/不相同(1/0)时的期望美观度
也挺好转移的(至少我赛时就想到了),我们循环两个量i, j(i:1 \sim n, j:0 \sim i – 1)
设sum = P_{i-j+1} \times (i-j)
第一种转移非常好写 dp_{i,1}+=dp_{j,0} \times sum
接下来稍微困难一点dp_{i,0}+=dp_{j,0} \times sum \times (m-2) + dp_{j,1} \times sum \times (m-1)
取答案时枚举首尾相接时的断点位置ans = P_n \times n + \sum_{i=1}^{n-1} f_{n-i,0} \times i \times i \times P_i
Code
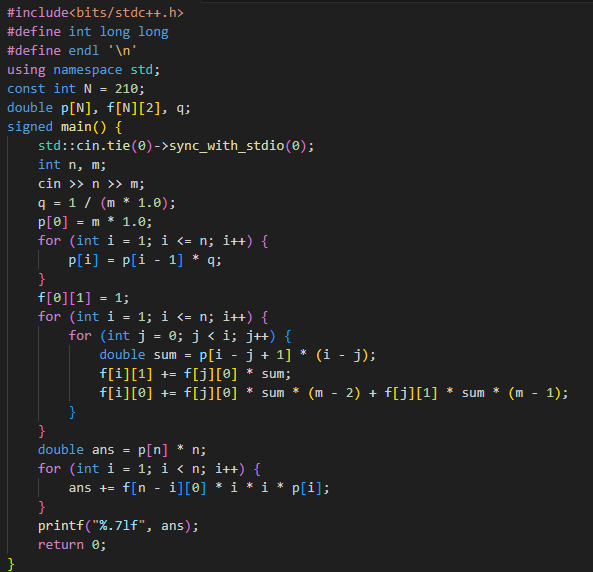
T2
设D_i为分摊伤害后i最终受到的伤害,$Ci自己真实受到的的伤害占总伤害的比例,T{i,j}表示i总共分给j的伤害的比例。那么D_i中除了第一次天降的伤害A_i$,其他伤害都是来源于别人的分摊,那么可以很轻(kun)松(nan)地推出一个式子:\frac{D_i}{C_i} = \sum_{i\ne j} \frac{D_j}{C_j}\times T_{i,j}+A_i
直接按照这个式子建立关于D_i的方程组,然后高斯消元解方程即可
Code
比较长,不放了,知道我AC了就好
T3
不会
T4
直接求割点,就是说跑一遍Tarjan,然后答案再做点小处理就好了
Code
比较长,不放了,知道我AC了就好
T5
好像是exgcd,但没打,赛时暴力30分