2025暑假中山集训Day11——8.05

题目描述
　因为对polo忍无可忍， dzf使用圣剑在地上划出了许多纵横交
错的沟壑来泄愤。这些沟壑都严格与X轴平行或垂直。
　polo嘲笑了dzf无聊的行为,然后做了一件更加无聊的事。他蹲
下来数这些沟壑的条数。数着数着，polo意识到一个问题,那就是
因为圣剑的威力太大，划出的沟壑太多,地面就会塌陷。而如果两
条水平的沟壑和两条垂直的沟壑相交组成了一个矩形,那么塌陷的
危险就会进一步增加。现在polo已经数了n条沟壑，他想知道这些
沟壑组成了多少个矩形。

输入
　第一行一个数n,接下来每行4个数x1,y1,x2,y2，表示沟壑的两
个端点(x1,y1),(x2,y2)

输出
　一个数，组成的矩形个数。

赛时思路：

暴力

赛时代码:

不想放

标程思路：

枚举两条垂直的线段，枚举一条水平的线段+设都与两条垂直线段相交的水平线段的数量为k，那么明显能构成 C(k,2)=\frac{k(k−1)}{2}个矩形

标程代码:

还没打，就不放了

题目描述
　圣玛格丽特大图书馆是一座由石材砌成的角柱型高塔，是欧洲
屈指可数的巨大书库。图书馆整面墙壁都是巨大的书架，书架与
书架之间就像巨大的迷宫一般，以细窄的木制楼梯连结。大图书
馆的最高处是一个绿意盎然的植物园，维多利加正在那无聊地看
着书。今天，一如往常地，久城要爬上这迷宫般的楼梯给维多利
加送讲义。
　图书馆墙壁上有N个平台，编号为1到N，入口为1号，植物园为
N号。有M个连接两个不同平台的楼梯，爬每个楼梯需要消耗一定
的体力值。楼梯一定是由低处通往高处的，为了省时间，久城只
能选择上楼梯而不能下楼梯，也就是说，楼梯之间不会形成环路
而且，出于人性化考虑，不管久城选择哪条路线上楼，他爬的楼
梯数量一定小于20。
　为了使体力消耗尽量平稳,久城需要选择一条“每个楼梯消耗体
力值的方差最小”的路径上楼。请帮助久城计算出这个最小方差.

输入
　第一行包含2个整数N,M，表示图书馆的平台数和楼梯数；
　接下来M行，每行3个数x,y,z，表示存在一条由平台x通往平
台y的楼梯，爬这个楼梯需要消耗z的体力值。

输出
　一行1个实数，表示最小方差，精确到小数点后4位。

赛时思路：

动态规划

具体内容见下文

赛时代码:

后来发现稍微一改就AC了，看下面的就好了

标程思路：

由计算平均数和方差公式可得 \bar{x} = \frac{\sum\limits_{i=1}\limits^{n}{a_{i}}}{n}，s^2=\frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\bar{x})^2}}{n}

在将 \bar{x} 带入可得 s^2=\frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\frac{\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n}

化简 \begin{aligned} \frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\frac{\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n} &= \frac{\sum\limits_{i=1}\limits^{n}{(\frac{na_{i}-\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{\frac{(na_{i})^2-2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}+(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^2}}}{n} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{((na_{i})^2-2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}+(\sum\limits_{j=1}\limits^{n}{a_{j}})^2)}}{n^3} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{n^2a_{i}^2}-\sum\limits_{i=1}\limits^{n}{2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}}+\sum\limits_{i=1}\limits^{n}{(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}}{n^3} \\ &= \frac{n^2\sum\limits_{i=1}\limits^{n}{a_{i}^2}-2n\sum\limits_{i=1}\limits^{n}{a_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}}+n(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^3} \\ &= \frac{n^2\sum\limits_{i=1}\limits^{n}{a_{i}^2}-2n(\sum\limits_{i=1}\limits^{n}{a_{i}})^2+n(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^3} \\ &= \frac{n\sum\limits_{i=1}\limits^{n}{a_{i}^2}-(\sum\limits_{i=1}\limits^{n}{a_{i}})^2}{n^2} \end{aligned}

可以发现 \sum\limits_{i=1}\limits^{n}{a_{i}^2} 和 \sum\limits_{i=1}\limits^{n}{a_{i}} 可以用前缀和优化，所以可以 O(1) 算出任意一个序列的方差

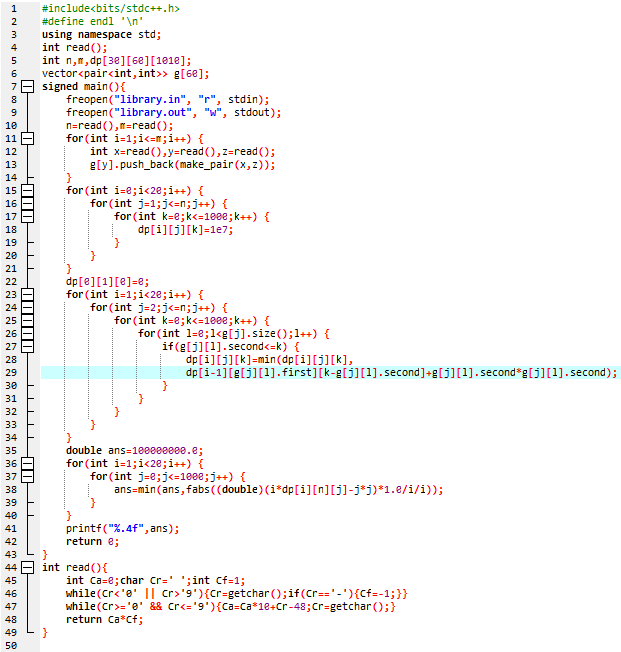
设 dp_{i,j,k} 走过了 i 条边，现在在 j 这个平台，经过的路程为 k 的最小平方和。

容易发现 dp_{i,j,k}=min(dp_{i,j,k},dp_{i-1,v,k-a_{v,j}}+a_{v,j}^2)

我们只需要枚举 v 进行转移，时间复杂度是 O(20000m)

标程代码:

没时间了，就不打了

没时间了，就不打了