21 Days Training // Day 11

T0. rect

My idea : enum.

Steps :

1. Select 2 horizontial/vertical segment.
2. Enum all vertical/horizontial segment.
3. If the segment in 2 intersects with both segments in 1, cnt++. (Here cnt records how many segments intersects with segemtns in 1.)
4. ans += cnt*(cnt-1)/2

Code :

#include <bits/stdc++.h>
using namespace std;

struct Segment {
    int sx, sy, ex, ey;
};

int main() {
    int N;cin >> N;
    vector<Segment> Vs0, Hs0;
    for (int i=0;i<N;i++) {
        int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;
        if (x1==x2) Vs0.push_back({min(x1, x2), min(y1, y2), max(x1, x2), max(y1, y2)});
        else Hs0.push_back({min(x1, x2), min(y1, y2), max(x1, x2), max(y1, y2)});
    }
    vector<Segment> Vs, Hs;
    if (Vs0.size()>Hs0.size()) Vs=Hs0, Hs=Vs0;
    else Vs=Vs0, Hs=Hs0; 
    long long ans=0;
    for (int i=0;i<Vs.size()-1;i++) {
        for (int j=i+1;j<Vs.size();j++) {
            long long isec=0;
            for (int k=0;k<Hs.size();k++) {
                if ((Hs[k].sx>Vs[i].sx)||(Hs[k].ex<Vs[i].sx)||(Vs[i].sy>Hs[k].sy)||(Vs[i].ey<Hs[k].sy)) continue;
                if ((Hs[k].sx>Vs[j].sx)||(Hs[k].ex<Vs[j].sx)||(Vs[j].sy>Hs[k].sy)||(Vs[j].ey<Hs[k].sy)) continue;
                isec++;
            }
            ans += isec*(isec-1)/2;
        }
    }
    cout << ans;
    return 0;
}

Complexity : worst : O(n^3)

Constraints :

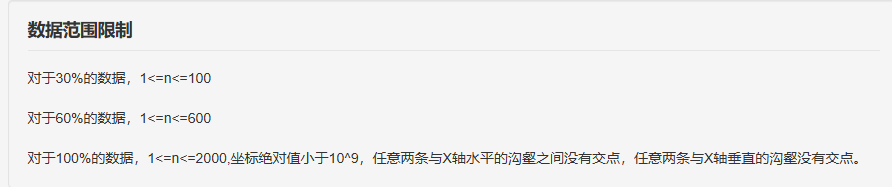
Expected : 60/30

(However, with the same idea, they can get 100, even it is not expected…)