今天是专题日，没比赛

裴蜀定理

原定理

对于a,b均为不为零的整数来说，对任意整数对(x,y)，满足gcd(a,b)|ax+by，且存在无数对整数对(x,y)，使得ax+by=gcd(a,b)

逆定理

若存在正整数d,满足d|a且d|b，且存在整数对(x,y)使得ax+by=d，则d=gcd(a,b)

推广定理及其逆定理

这是改写过后的定理

对于向量A=(a1,a2,…,an)，其中ai为不为0的整数，必有向量X=(x1,x2,…,xn)，其中xi为整数，满足A与X的的内积为gcd(a1,a2,…,an)

其逆定理表述为，若有正整数d满足d|任意ai，又存在X使得其与A的内积为d，则d=gcd(a1,a2,…,an)

练习Luogu P4549

LINK

本体显然由裴蜀定理可知，要求的就是gcd(a1,a2,…,an)，代码也很简洁

注意，求出来的ans可能为负数，因此要取绝对值

数论练习

T1 GCD SUM

数据范围

时间复杂度目标O(n)或O(nlog(n))

看了题解发现有两种做法，都很不错

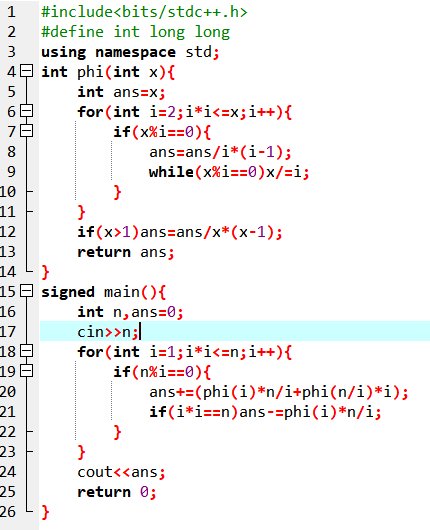
法一 欧拉反演

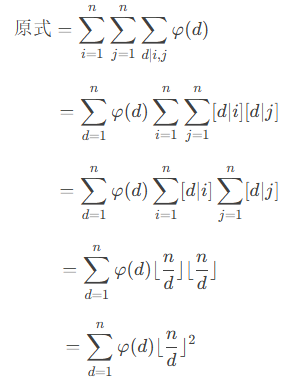
这样一来枚举d即可O(n)通过(欧拉函数用线性筛处理)

Code:

法二 改写原式

对于代码实现，我们要从后往前枚举，才能保证f[i]的值更新不会遗漏，以及时间复杂度为O(nH(n))

对于时间复杂度：
事实上H(n)-1=1/2+1/3+..+1/n < log(n)
可以积分放缩证明

所以时间复杂度完全是没问题的

Code:

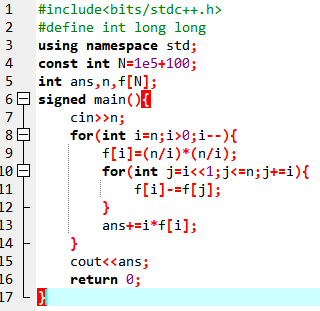
该方法虽然时间复杂度并不优于线性复杂度，但是码量超小

T2 GCD

我的想法，对于素数p来说phi(p)=p-1所以我们可以用这个来判断，原题等价于求多少组(i,j)满足phi(gcd(i,j))=gcd(i,j)-1，然后推式子

但是刚开始就推不下去了，说明这个思路是有问题的

来看题解吧

这个套路式变形学到了

那就很好打了，几乎板题

T3 乘法逆元 Luogu P3811

乘法逆元的其它解法详见OI Wiki————乘法逆元

本题需要使用线性求乘法逆元，原理如下

要求1~n在模p(p是质数)的乘法逆元，我们假设求解到第i个

设k=i/p(下取整),j=i mod p
则 ki+j = 0 (mod p)
(ki+j)(j^-1)(i^-1) = 0 (mod p)
k(j^-1)+i^-1 = 0 (mod p)
i^-1 = -k(j^-1) (mod p)
对于i=1,i^-1=1 (mod p)

Code：

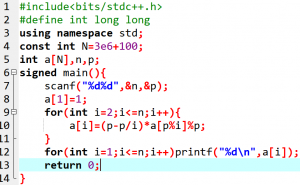
T4 有理数取余

来看数据范围

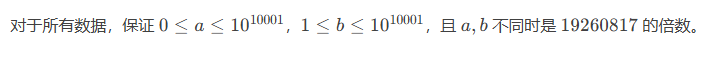
是不是觉得要高精度？
事实上变形一下就会发现我们再求这样一个同余方程，下记模数为P，事实上这个数是质数

bx=a (mod P)
(b mod P)x=(a mod P) (mod P)
x=(a mod P)((b mod P)^-1) (mod P)

这样我们用字符读入的时候就可以取模，把a和b的范围缩小
再用费马小定理（快速幂）求乘法逆元即可

注意最后还要再模一次P

Code：

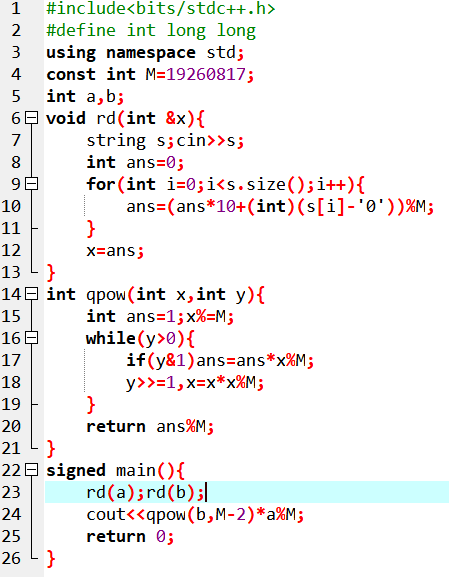
T5 同余方程 Luogu P1082

我觉得这题可以当成扩欧求乘法逆元的板题了

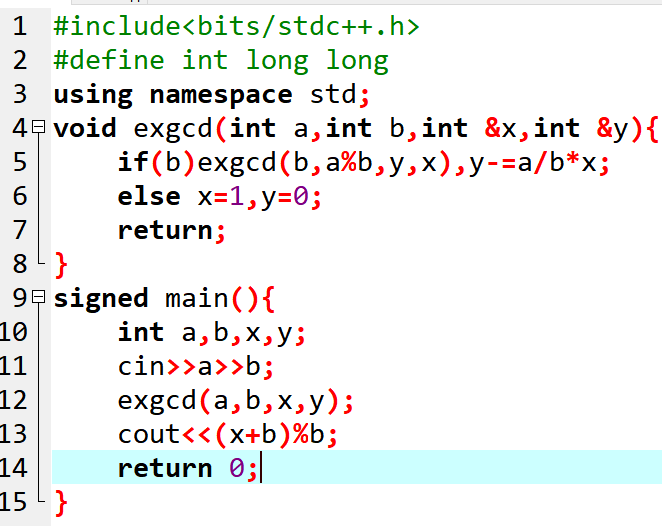
T6 Longge 的问题 Luogu P2303

这题是练习欧拉反演的基础题，我认为也可以作为O(sqrt(n))求欧拉函数的模板题

先看数据范围

这题O(sqrt(n))可以通过，先推式子，这个OI Wiki上有————Link

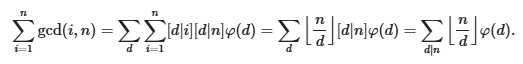
我们可以O(sqrt(n))求解其因数以及因数的欧拉函数
总时间复杂度为O(d(n)*sqrt(n))

晚自习

打点图论题

T1 P1828 [USACO3.2] 香甜的黄油 Sweet Butter

直接Johnson模板往上套，改几个地方就行（由于边权是正的，连spfa和rebuild都不用）

太简单，代码不放了

T2 P1821 [USACO07FEB] Cow Party S

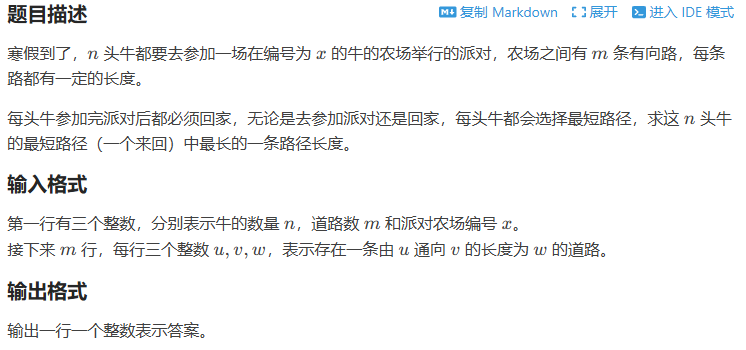
这题可以存反图，分别求出x到各点在正图和反图中的最小距离，再加起来，及来回距离，最后比个大小就行

太简单，代码不放了

OK，这就是今日所有内容（事实上是懒得继续写了），goodbye