21 Days Training // Day (8 2/3)~(9 2/3)

T1. dragon

Notice that the sword used every turn is constant.
And in every turn, to kill the dragon, attack count x , ATK A , Initial HP h , recovery HP r satisfies Ax \equiv h \pmod{r} .
S0, for every dragon, solve the equation above, merge the solves fo equations, and then find the mininum number of X;
Notice that when r=1, we should directly skip this equation.
However, I cannot write exgcd()…
But there is still 20:

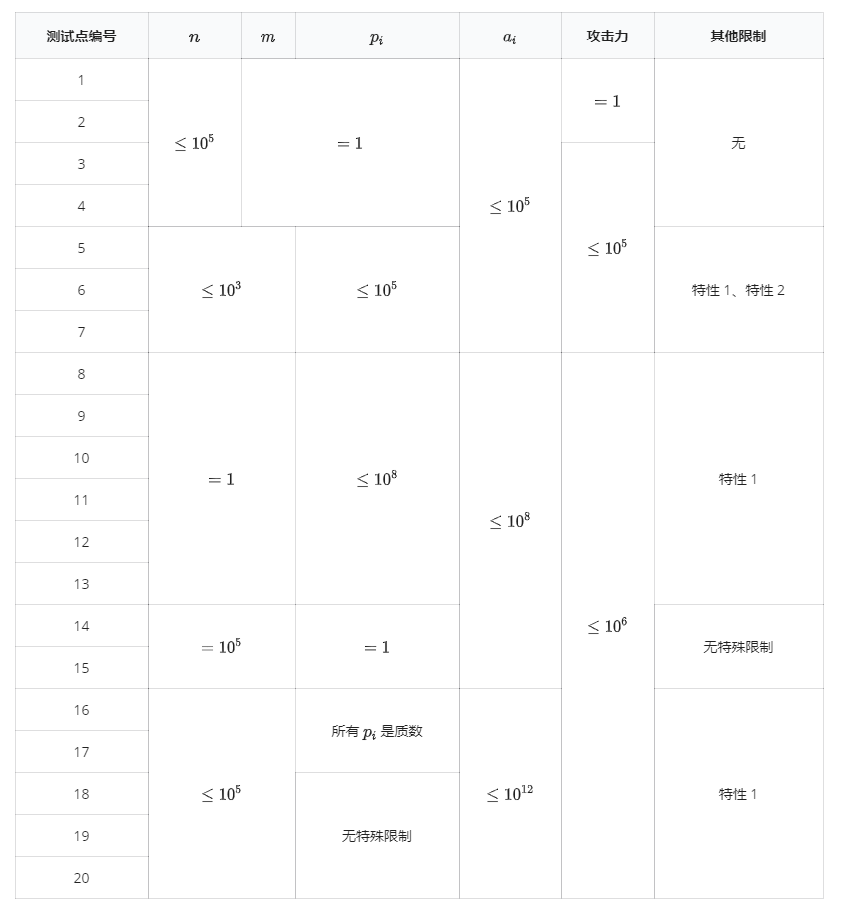
For case 1~4, we can directly compute the mininum value of HP.
And when you get exgcd, you can get the score of case 8~13.
Expected : 20/50

Code :

/* SWORD */
#include <bits/stdc++.h>
using namespace std;

//inv -del
void exgcd(long long a, long long b, long long& x, long long& y) {
    if (b == 0) {
        x = 1, y = 0;
        return;
    }
    exgcd(b, a % b, y, x);
    y -= a / b * x;
}

void SWORD() {
    long long N, M;cin >> N >> M;
    long long HP[N], RC[N], RW[N];
    for (int i=0;i<N;i++) cin >> HP[i];
    for (int i=0;i<N;i++) cin >> RC[i];
    for (int i=0;i<N;i++) cin >> RW[i];
    vector<long long> ATK_i;
    for (int i=0;i<M;i++) {
        int X;cin >> X;
        ATK_i.push_back(X);
    }
    sort(ATK_i.begin(), ATK_i.end());
    long long ATK[N];
    for (int i=0;i<N;i++) {
        int pos=lower_bound(ATK_i.begin(), ATK_i.end(), HP[i])-ATK_i.begin();
        if (pos!=0) pos--;
        ATK[i] = ATK_i[pos];
        ATK_i.erase(ATK_i.begin()+pos);
        int npos=lower_bound(ATK_i.begin(), ATK_i.end(), RW[i])-ATK_i.begin();
        ATK_i.insert(ATK_i.begin()+npos, RW[i]);
    }
    long long K=1, B=0, minx=0;
    for (int i=0;i<N;i++) {
        long long sc=ATK[i], r=HP[i], MOD=RC[i];
        minx = max(minx, (long long)ceil(HP[i]/(double)ATK[i]));
        if (MOD==1) continue;
        else {
            long long nsc=sc*K, nr=r-sc*B;
            if (nr%__gcd(nsc, MOD)) {
                cout << -1 << endl;
                return ;
            }
            long long nsc2=nsc/__gcd(nsc, MOD), nr2=nr/__gcd(nsc, MOD), nMOD=MOD/__gcd(nsc, MOD);
            long long inv, _;
            exgcd(nsc2, nMOD, inv, _);
            inv+=nMOD;
            nr2 *= inv;
            // x equiv nr2 * inv (mod nMOD)
            // G : kx+b
            // G&#039; : k(nMODx+nr2)+b
            B = K * nr2 + B; 
            K *= nMOD;
        }
    }
    long long Smin = ceil((minx-B)/(double)K);
    cout << K*Smin+B << endl;
}

int main() {
    long long T;cin >> T;
    for (long long i=0;i<T;i++) SWORD();
    return 0;
}