昨晚ABC
也是脑子宕机了,C题明明已经把式子移项了,很简单的O(n)算法,没看出来,打暴力试图卡过,想了一个多小时,后面的题目没来得及看,赛后看别人代码瞬间恍然大悟,一下就改出来了,于是总分只有可怜的300分
早上比赛
今天上午打了110,依旧把T1拿下,但是后面T2几乎半个板题,但没背,痛失100
T1 有趣的家庭菜园

大概翻译一下就是求要将一个序列,经过多少次对某段区间内元素加一后,形成的新序列先单调递增,再单调递减(也可以是一个单调递增的序列或单调递减的序列)(是不是想起了合唱队形)
显然答案的贡献应该与相邻两数之差有关,考虑dp
设dp1[i]表示到第i位时,使得a1~ai单调递增的最小操作次数,dp2[i]表示到第i位时,使得ai到an单调递减的最小操作次数,那么若ai是最高的那个,那么操作次数即
min(dp1[i],dp2[i])
状态转移方程(伪核心代码):
if a[i] dp1[i]=dp1[i-1]+a[i-1]-a[i]+1,
else dp1[i]=dp1[i-1].
if a[i] dp2[i]=dp2[i+1]+a[i+1]-a[i]+1,
else dp2[i]=dp2[i+1].
ans=min(ans,max(dp1[i],dp2[i]))
Code:
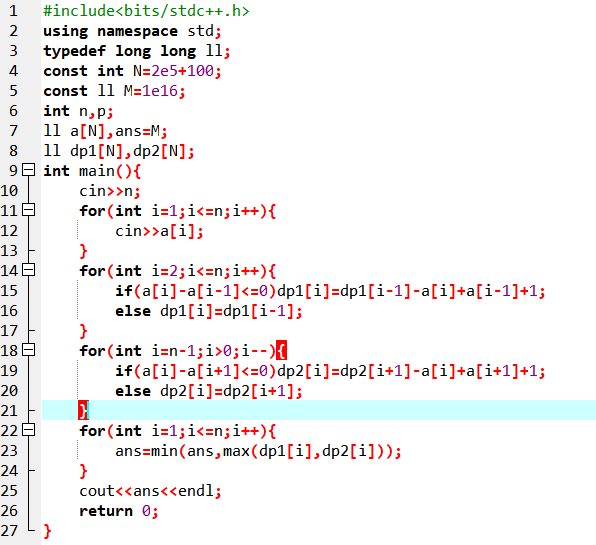
细节:dp1要从前往后更新,dp2要从后往前更新,不等号方向别写错了
T2 屠龙勇士
本题多测 Luogu P4774

一眼数论题,一眼解线性同余方程组,但没背板就是不会做
题解看了,发现还要学点其他知识
需要学习的知识:
线性同余方程组求解(中国剩余定理)
multiset
龟速乘
_int128
Code:

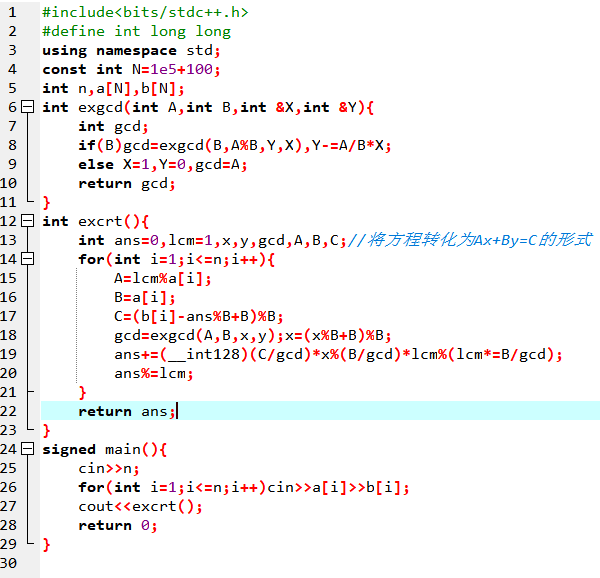
这里给出扩展中国剩余定理的模板(含扩欧模板),这是根据题解提炼出的更加一般化的形式,可以将同余方程组转换为如Ax+By=C形式后求解,x前的系数不必为1
模板
晚上ARC
猎奇,T1找规律找了一个多小时
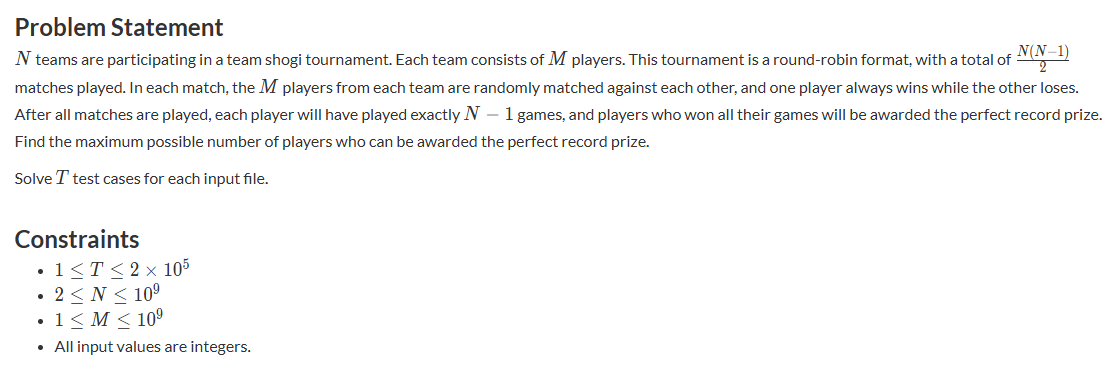
T1 All Winners
做一篇英语阅读吧
翻译:给出n个队伍,每支队伍有m个队员,每位队员会参加(n-1)场比赛,并对到其他队的不同队员,一个队员只会对到其他(n-1)支队伍各一次,问最多有对少队员可以赢下(n-1)场比赛
这个需要画图解释会好些
下面以n=3,m=3为例
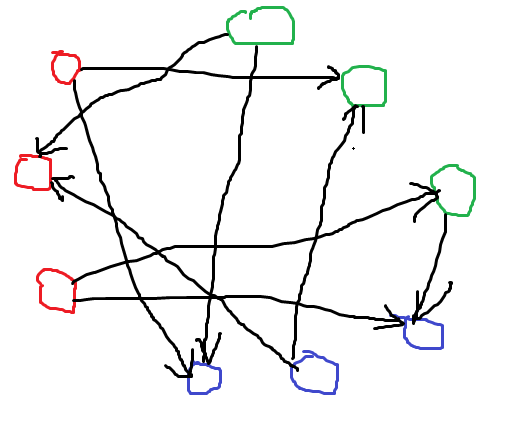
再以n=3,m=4为例
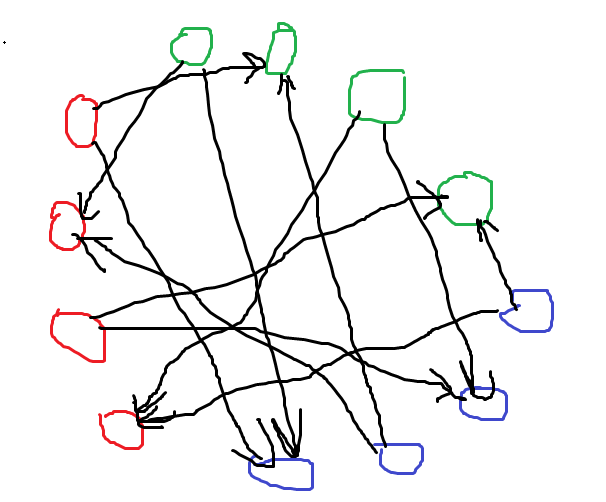
(说明,每个小圈代表一个队员,不同颜色代表不同队伍,败者向胜者连有向边)
不难看出,同样的结构反复出现,如下
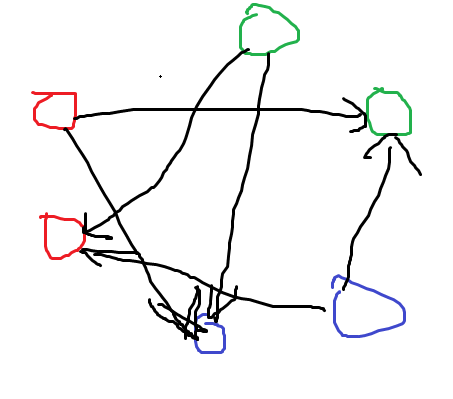
对于这个图,共有3个队员满足条件
若记f(n,m)为满足条件的队员最大数量,不难得到
f(n,2)=n,
再利用此结构反复出现,不难得出
if m mod 2=0 f(n,m)=nm/2
else f(n,m)=n(m-1)/2+1
这样就能AC此题
Code:
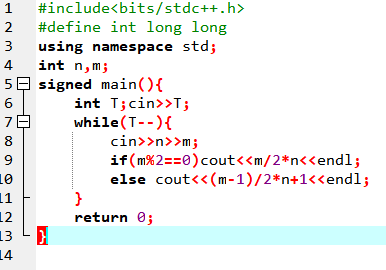
注意要换行
其他题没打了,没有时间了