早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
打比赛—-2025.08.01【提高B组】模拟赛
又少了80分
传送门
T1
题目描述
Winter is coming.
Robert 是个昏庸的君主,整日沉迷于吃喝玩乐,终于,当寒冬
降临,他不得不组织军队来对抗敌人。
尽管如此,他仍然是个喜欢玩耍的人,还有点强迫症,他希望选出
的军队的所有人的身高的方差最小,并且选出的人数x要满足 L<=x
<=R,因为太少了他怕不够气势,太多了他怕会控制不当。
现在给出 n 个士兵的高度,L 和 R,Robert 找到聪明的你,
希望你帮他解决这个难题。
输入
第一行三个整数,依次是 n, L, R
第二行 n 个正整数,表示每个士兵的高度 h
输出
一行,表示最小的方差,保留三位小数即可。
赛时思路:
由计算平均数和方差公式可得 \bar{x} = \frac{\sum\limits_{i=1}\limits^{n}{a_{i}}}{n},s^2=\frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\bar{x})^2}}{n}
在将 \bar{x} 带入可得 s^2=\frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\frac{\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n}
化简 \begin{aligned} \frac{\sum\limits_{i=1}\limits^{n}{(a_{i}-\frac{\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n} &= \frac{\sum\limits_{i=1}\limits^{n}{(\frac{na_{i}-\sum\limits_{j=1}\limits^{n}{a_{j}}}{n})^2}}{n} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{\frac{(na_{i})^2-2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}+(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^2}}}{n} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{((na_{i})^2-2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}+(\sum\limits_{j=1}\limits^{n}{a_{j}})^2)}}{n^3} \\ &= \frac{\sum\limits_{i=1}\limits^{n}{n^2a_{i}^2}-\sum\limits_{i=1}\limits^{n}{2na_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}}+\sum\limits_{i=1}\limits^{n}{(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}}{n^3} \\ &= \frac{n^2\sum\limits_{i=1}\limits^{n}{a_{i}^2}-2n\sum\limits_{i=1}\limits^{n}{a_{i}\sum\limits_{j=1}\limits^{n}{a_{j}}}+n(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^3} \\ &= \frac{n^2\sum\limits_{i=1}\limits^{n}{a_{i}^2}-2n(\sum\limits_{i=1}\limits^{n}{a_{i}})^2+n(\sum\limits_{j=1}\limits^{n}{a_{j}})^2}{n^3} \\ &= \frac{n\sum\limits_{i=1}\limits^{n}{a_{i}^2}-(\sum\limits_{i=1}\limits^{n}{a_{i}})^2}{n^2} \end{aligned}
可以发现 \sum\limits_{i=1}\limits^{n}{a_{i}^2} 和 \sum\limits_{i=1}\limits^{n}{a_{i}} 可以用前缀和优化,所以可以 O(1) 算出任意一个序列的方差
再暴力枚举开头为 i ,长度为 l \sim r 的字符串,计算方差,输出最小值即可
时间复杂度 O(n^2)
赛时代码:

标程思路:
可以发现,任意一个序列,它加上一个新元素不会使得其方差更优。
所以,序列的长度只能是 l,从 1 到 n-l+1 枚举一遍即可
时间复杂度 O(n)
标程代码:

T2
题目描述
Ned 再也看不下去 Robert 的种种恶习,于是他决定出一道题
来让他醒悟。
Ned 的题目是这样:
给出一个有 n 个数的序列,求其中所有连续子序列的数的最大
公因数的乘积模 1000000009 的值。
Robert 当时就立刻给出了一个超级无敌速度无人能及的O(1)错
误解法。
既然 Robert 不会做,Ned 决定让你来做出这题来证明Robert
不应颓废下去。
输入
第一行一个正整数 n(1≤n≤50000)
第二行 n 个正整数 a [i](1≤a [i]≤10000000)
输出
一行一个整数表示序列中所有连续子序列的数的最大公因数的
乘积模 1000000009 的值
赛时思路:
n^2 暴力枚举
赛时代码:

标程思路:
首先列出数学式子:ans=\prod\limits_{i=1}\limits^{n}{\prod\limits_{i=1}\limits^{n}{gcd(a_i,a_{i+1},\dots,a_{j-1},a_j)}}
们来看一下 gcd 的本质,举个例子,有两个数,一个是12,一个是18,那么他们的 gcd 是 6,那么 6 是怎么得到的呢?
\begin{aligned}12 &= 2^2 \times 3^1,\quad 18 = 2^1 \times 3^2 \\ \gcd(12, 18) &= 2^{\min(2, 1)} \times 3^{\min(1, 2)} \\ &= 2^1 \times 3^1 = 6 \end{aligned}
所以某个质数 p 对答案的贡献跟一个子序列里这个质数的次数的最小值有关,即 p^{min(a_i)},观察到最终求的是 gcd 的乘积,所以,我们可以现将所有数分解质因数,然后对于一个质数对某个区间的答案的贡献,其实就是这个区间内这个质数的次数的最小值,所以我们可以用笛卡尔树加上快速幂来解决,时间复杂度 O(8n \log n) (注,有常数 8 是因为每个小于 10^7 数最多可以被分成八个不同的质因数)
标程代码:
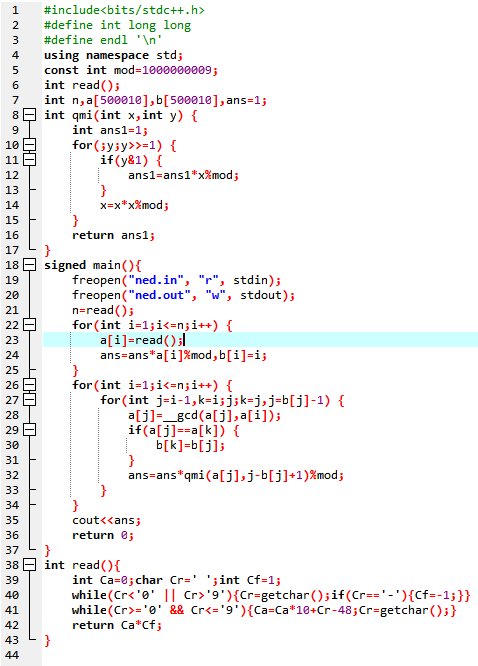
T3
题目描述
YYC最近在和旅店老板的对战中被虐惨了,关键时刻,他打出了
“生命之树”为自己续秒。
生命之树是一张有 n 个节点的无向无环图,其中1号节点为根.
每个节点上有一个由小写字母组成的符咒 S_i和一个权值val_i,
但只有两个不同的符咒组合起来才会为他续秒,而两个符咒的收益
(能够续的秒数)w(S_i, S_j) 正是这两个字符串的最长公共前
缀的长度。
定义 dec_u 为 u 的后代集合(特别地,u \in dec_u),那
么以 u 为根的子树的总收益为:ans_u = \sum_{\substack{i
\in dec_u \\ j \in dec_u \\ i < j}} (val_i \text{xor
} val_j) \times w(S_i, S_j)
其中 xor 代表异或运算。
由于使用生命之树的花费是巨大的,YYC决定只使用生命之树的
某个子树。他需要知道对于每个节点 u,以 u 为根的子树的总收
益是多少。
输入
第一行一个整数 n,表示点数。
接下来1行,n 个整数表示 val_i。
接下来 n 行,每行一个字符串表示 S_i。
接下来 n - 1 行,每行两个整数 u, v,表示 u, v 之间有
一条边。
输出
输出 n 行,每行一个整数表示 ans_i。
赛时思路:
暴力
赛时代码:
没时间,不放了
标程思路:


标程代码:
没打,就不放了
T4
题目描述
第一天的第一题,一般都是一道送分的大水题,这次也不例外.
给定 n 个 m 维向量,每一维的取值只能是 1 或 2 或 3 或
4。接下来有 q 个询问,每个询问都是这四种询问中的一种:
(1)给定一个向量 C,问有多少种方法从这 n 个向量中选出
2 个向量 A 和 B,使得对于每一维 i(1 ≤i ≤ m),A i和B i
的最大值小于等于 C i 。
(2)给定一个向量 C,问有多少种方法从这 n 个向量中选出
2 个向量 A 和 B,使得对于每一维 i(1 ≤i ≤ m),A i和B i
的最小值大于等于 C i 。
(3)给定一个向量 C,问有多少种方法从这 n 个向量中选出
2 个向量 A 和 B,使得对于每一维 i(1 ≤i ≤ m),A i和 B i
的最大值大于等于 C i 。
(4)给定一个向量 C,问有多少种方法从这 n 个向量中选出
2 个向量 A 和 B,使得对于每一维 i(1 ≤i ≤ m),A i 和B i
的最小值小于等于 C i 。
其中,C 也是一个 m 维向量,并且每一维的取值也只能是 1
或 2 或 3 或 4。A i 表示向量 A 的第 i 维的值,B i和C i
同理。
为了更加准确地说明“多少种方法”的含义,我们规定:令第i次
读入的向量为第 i 个向量,那么一种方法就对应一个集合 {i,j}
(i 不等于 j),两种方法不是同一种方法,当且仅当它们对应
的集合 {i,j} 不相同。
输入
第一行两个整数 n 和 m,表示接下来会有 n 个 m 维向量。
接下来 n 行,每行一个长度为 m 的字符串,每个字符串表示
一个向量,第 i 个字符表示第 i 维的值。
接下来一行是一个整数 q,表示询问的个数。
接下来 q 行,每行一个询问,包含一个整数 t 和一个字符串,
其中 t 表示是哪一种询问,字符串表示给定的向量 C。
输出
输出共有 q 行。对于每个询问,输出一行,包含一个整数,表
示方案数。
赛时思路:
暴力
赛时代码:
没时间,不放了
标程思路:

