21 Days Training // Day 7

0. army

One key conclusion :

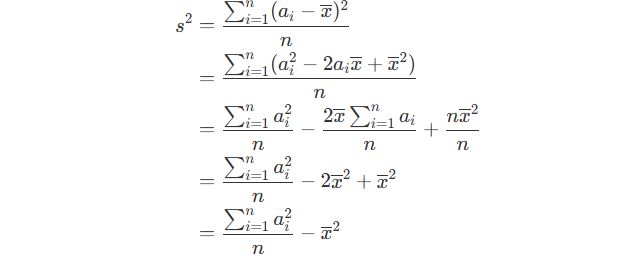
However, for me, I will stop at this conclusion and enumrate all possible plans, making a algorithm with a complexity of O(n2^n) .

But, if we continue :

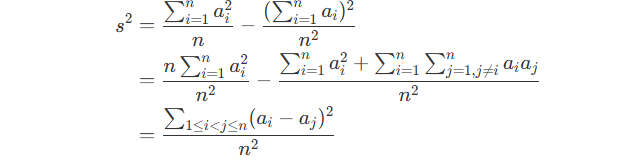
From this, we can get more conclusions :

1. After sorting this array, we must select a continuous region.
2. The length of this region must be L.

Since $ \sum_{i=1}^n ai^2 and \sum{i=1}^n a_i can be preprocessed with a complexity of O(n) $, we can easily pass this problem.

AC Code :

#include <bits/stdc++.h>
using namespace std;
/* NOT MY CODE. */

int main() {
    freopen("army.in", "r", stdin);
    freopen("army.out", "w", stdout);
    int N, L, R;cin >> N >> L >> R;
    double A[N], sqsum_pfx[N+1], sum_pfx[N+1];
    sqsum_pfx[0] = sum_pfx[0] = 0;
    for (int i=0;i<N;i++) {
        cin >> A[i];
    }
    sort(A, A+N);
    for (int i=0;i<N;i++) {
        sqsum_pfx[i+1] = sqsum_pfx[i] + A[i]*A[i];
        sum_pfx[i+1] = sum_pfx[i] + A[i];
    }
    double var=1.797e+308;
    for (int i=0;i<=N-L;i++) {
        var = min(var, (double)(sqsum_pfx[i+L]-sqsum_pfx[i])/L - (double)(sum_pfx[i+L]-sum_pfx[i])*(sum_pfx[i+L]-sum_pfx[i])/(L*L));
    }
    printf("%.3lf", var);
    return 0;
}