早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
讲算法和学算法
1. 李超线段树
引入
洛谷 4097 [HEOI2013]Segment
要求在平面直角坐标系下维护两个操作(强制在线):
- 在平面上加入一条线段。记第 i 条被插入的线段的标号为 i,该线段的两个端点分别为 (x_0,y_0),(x_1,y_1)。
- 给定一个数 k,询问与直线 x = k 相交的线段中,交点纵坐标最大的线段的编号(若有多条线段与查询直线的交点纵坐标都是最大的,则输出编号最小的线段)。特别地,若不存在线段与给定直线相交,输出 0。
数据满足:操作总数 1 \leq n \leq 10^5,1 \leq k, x_0, x_1 \leq 39989,1 \leq y_0, y_1 \leq 10^9。
我们发现,传统的线段树无法很好地维护这样的信息。这种情况下,李超线段树 便应运而生。
过程
我们可以把任务转化为维护如下操作:
- 加入一个一次函数,定义域为 [l,r];
- 给定 k,求定义域包含 k 的所有一次函数中,在 x=k 处取值最大的那个,如果有多个函数取值相同,选编号最小的。
注意
当线段垂直于 x 轴时,会出现除以零的情况。假设线段两端点分别为 (x,y_0) 和 (x,y_1),y_0<y_1,则插入定义域为 [x,x] 的一次函数 f(x)=0\cdot x+y_1。
看到区间修改,我们按照线段树解决区间问题的常见方法,给每个节点一个懒标记。每个节点 i 的懒标记都是一条线段,记为 l_i,表示要用 l_i 更新该节点所表示的整个区间。
现在我们需要插入一条线段 f,考虑某个被新线段 f 完整覆盖的线段树区间。若该区间无标记,直接打上用该线段更新的标记。
如果该区间已经有标记了,由于标记难以合并,只能把标记下传。但是子节点也有自己的标记,也可能产生冲突,所以我们要递归下传标记。
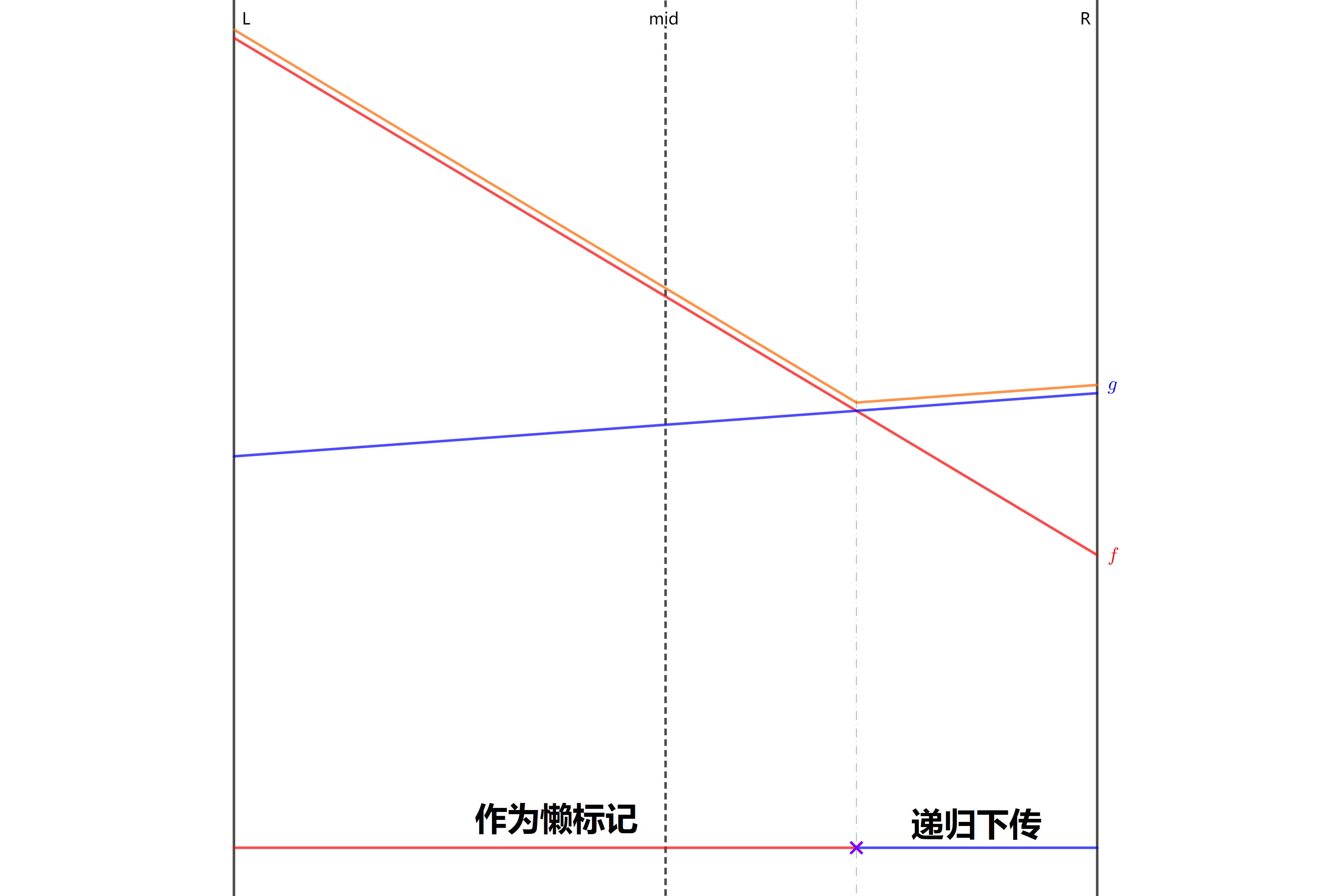
如图,按新线段 f 取值是否大于原标记 g,我们可以把当前区间分为两个子区间。其中 肯定有一个子区间被左区间或右区间完全包含,也就是说,在两条线段中,肯定有一条线段,只可能成为左区间的答案,或者只可能成为右区间的答案。我们用这条线段递归更新对应子树,用另一条线段作为懒标记更新整个区间,这就保证了递归下传的复杂度。当一条线段只可能成为左或右区间的答案时,才会被下传,所以不用担心漏掉某些线段。
具体来说,设当前区间的中点为 m,我们拿新线段 f 在中点处的值与原最优线段 g 在中点处的值作比较。
如果新线段 f 更优,则将 f 和 g 交换。那么现在考虑在中点处 f 不如 g 优的情况:
- 若在左端点处 f 更优,那么 f 和 g 必然在左半区间中产生了交点,f 只有在左区间才可能优于 g,递归到左儿子中进行下传;
- 若在右端点处 f 更优,那么 f 和 g 必然在右半区间中产生了交点,f 只有在右区间才可能优于 g,递归到右儿子中进行下传;
- 若在左右端点处 g 都更优,那么 f 不可能成为答案,不需要继续下传。
除了这两种情况之外,还有一种情况是 f 和 g 刚好交于中点,在程序实现时可以归入中点处 f 不如 g 优的情况,结果会往 f 更优的一个端点进行递归下传。
最后将 g 作为当前区间的懒标记。
下传标记:
实现

拆分线段:
实现

注意懒标记并不等价于在区间中点处取值最大的线段。
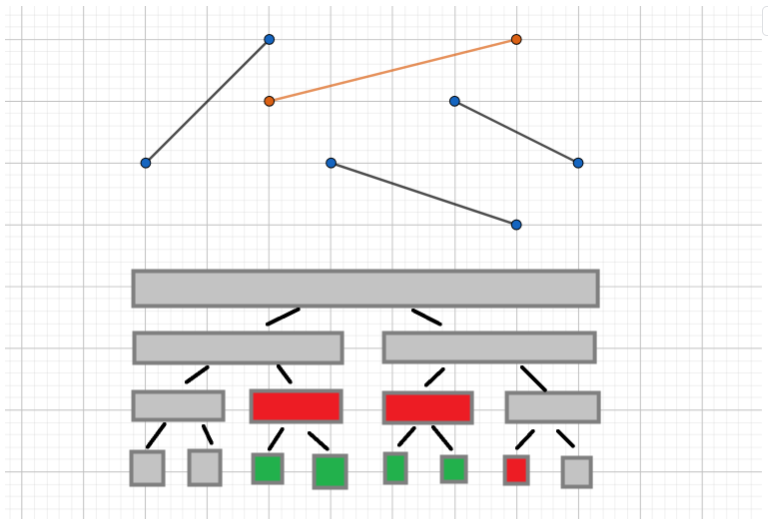
如图,加入黄色线段后,只有红色节点的标记被更新,而绿色节点的标记还未被改变。但在第二、三、四个绿色区间的中点处显然黄色线段取值最大。
查询时,我们可以利用标记永久化思想,在包含 x 的所有线段树区间(不超过 \log n 个)的标记线段中,比较得出最终答案。
查询:
实现
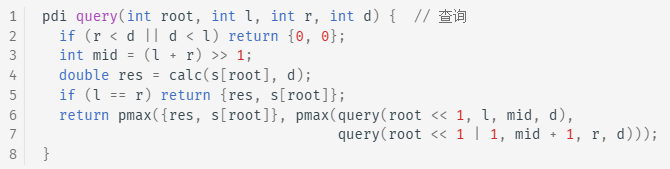
根据上面的描述,查询过程的时间复杂度显然为 O(\log n),而插入过程中,我们需要将原线段拆分到 O(\log n) 个区间中,对于每个区间,我们又需要花费 O(\log n) 的时间递归下传,从而插入过程的时间复杂度为 O(\log^2 n)。
合并
类似于普通线段树的合并,我们定义以下过程来将两个李超线段树节点 u,v 合并,作为新的根。
- 如果 v 为空,结束过程。
- 如果 u 为空,将 v 复制给 u。
- 将 v 对应线段插入到 u 为根的子树。
- 递归将 u,v 的左右子树对应合并。
若合并若干李超线段树涉及的总点数为 n,则该过程的复杂度为 O(n\log n):对于任意线段在树上对应的节点,每次涉及移动它时,我们要么使其深度 +1,要么直接从树上删除,这两个操作的代价都是 O(1) 的,而每个点深度至多为 O(\log n),于是复杂度如上。
实现

习题
本小节取自 OI-WIKI
2. 强连通分量
简介
强连通的定义是:有向图 G 强连通是指,G 中任意两个结点连通。
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
Tarjan 算法
引入
Robert E. Tarjan(罗伯特·塔扬,1948~),生于美国加州波莫纳,计算机科学家。
Tarjan 发明了很多算法和数据结构。不少他发明的算法都以他的名字命名,以至于有时会让人混淆几种不同的算法。比如求各种连通分量的 Tarjan 算法,求 LCA(Lowest Common Ancestor,最近公共祖先)的 Tarjan 算法。并查集、Splay、Toptree 也是 Tarjan 发明的。
DFS 生成树
在介绍该算法之前,先来了解 DFS 生成树,我们以下面的有向图为例:
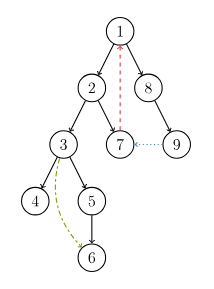
有向图的 DFS 生成树主要有 4 种边(不一定全部出现):
- 树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 反祖边(back edge):示意图中以红色边表示(即 7 \rightarrow 1),也被叫做回边,即指向祖先结点的边。
- 横叉边(cross edge):示意图中以蓝色边表示(即 9 \rightarrow 7),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
- 前向边(forward edge):示意图中以绿色边表示(即 3 \rightarrow 6),它是在搜索的时候遇到子树中的结点的时候形成的。
我们考虑 DFS 生成树与强连通分量之间的关系。
如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点,那么这个强连通分量的其余结点肯定是在搜索树中以 u 为根的子树中。结点 u 被称为这个强连通分量的根。
证明
反证法:假设有个结点 v 在该强连通分量中但是不在以 u 为根的子树中,那么 u 到 v 的路径中肯定有一条离开子树的边。但是这样的边只可能是横叉边或者反祖边,然而这两条边都要求指向的结点已经被访问过了,这就和 v 不在以 u 为根的子树中矛盾了。得证。
Tarjan 算法求强连通分量
Tarjan 算法基于对图进行 深度优先搜索。我们视每个连通分量为搜索树中的一棵子树,在搜索过程中,维护一个栈,每次把搜索树中尚未处理的节点加入栈中。
在 Tarjan 算法中为每个结点 u 维护了以下几个变量:
1. \textit{dfn}_u:深度优先搜索遍历时结点 u 被搜索的次序。
2. \textit{low}_u:在 u 的子树中能够回溯到的最早的已经在栈中的结点。设以 \textit{u} 为根的子树为 \textit{Subtree}_u。\textit{low}_u 定义为以下结点的 \textit{dfn} 的最小值:\textit{Subtree}_u 中的结点;从 \textit{Subtree}_u 通过一条不在搜索树上的边能到达的结点。
一个结点的子树内结点的 dfn 都大于该结点的 dfn。
从根开始的一条路径上的 dfn 严格递增,low 严格非降。
按照深度优先搜索算法搜索的次序对图中所有的结点进行搜索,维护每个结点的 dfn 与 low 变量,且让搜索到的结点入栈。每当找到一个强连通元素,就按照该元素包含结点数目让栈中元素出栈。在搜索过程中,对于结点 u 和与其相邻的结点 v(v 不是 u 的父节点)考虑 3 种情况:
1. v 未被访问:继续对 v 进行深度搜索。在回溯过程中,用 \textit{low}_v 更新 \textit{low}_u。因为存在从 u 到 v 的直接路径,所以 v 能够回溯到的已经在栈中的结点,u 也一定能够回溯到。
2. v 被访问过,已经在栈中:根据 low 值的定义,用 \textit{dfn}_v 更新 \textit{low}_u。
3. v 被访问过,已不在栈中:说明 v 已搜索完毕,其所在连通分量已被处理,所以不用对其做操作。
对于一个连通分量图,我们很容易想到,在该连通图中有且仅有一个 u 使得 \textit{dfn}_u=\textit{low}_u。该结点一定是在深度遍历的过程中,该连通分量中第一个被访问过的结点,因为它的 dfn 和 low 值最小,不会被该连通分量中的其他结点所影响。
因此,在回溯的过程中,判定 \textit{dfn}_u=\textit{low}_u 是否成立,如果成立,则栈中 u 及其上方的结点构成一个 SCC。
实现

时间复杂度 O(n + m)。
分量标号和拓扑序的关系
Tarjan 算法在处理过程中,实际上是按照某种 逆拓扑序 来发现强连通分量的,这是因为算法在深度优先搜索的过程中会先访问那些没有出边的节点,而这与拓扑排序的过程是相反的。
如果我们将图中的所有强连通分量缩成单个节点,那么在这些缩点后的节点形成的 DAG 中进行拓扑排序,得到的顺序将与 Tarjan 算法给出的强连通分量的标号顺序相反。
因此,可以说,在缩点后的 DAG 中,强连通分量(缩点后)的标号顺序是其拓扑序的逆序。但要注意的是,这种说法仅在考虑了强连通分量之间的依赖关系(即从一个强连通分量到另一个强连通分量的有向边)时才成立。单个强连通分量内部的节点由于存在环,所以内部并不满足拓扑序的定义。
本小节取自 OI-WIKI

