21 Days Training // Day 6

T2. Divisor Sum

Warning : This code may exceed the time limit(1s). Do not try!

Notice that the divisor sum \sigma(\Pi_{i=1}^k p_i^{q_i}) satisfies :

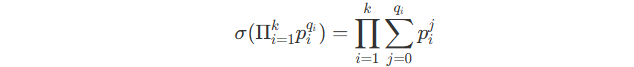
And :

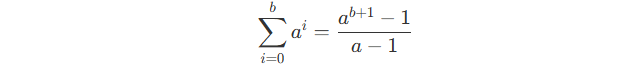
So we can first decompose a^b to get prime factors, and then for the factors, use equation 2 to compute the sum term in property 1 quickly, and mod the result every step.

However, the modulo operation and makes sense in addition, substraction, and multiplication, how to deal with the term \frac{1}{a-1} ?

Here comes the now conception : the inversion under modulo operation.

If for a number a , x satisfies :

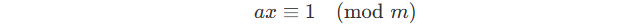
Wa call x an inversion of a under modulo m .
However, if we directly divide LHS and RHS by a …

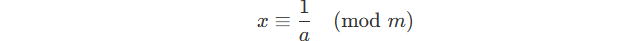
We get the modulo of a division operation!
Now we need to get x quickly…
Notice that the modulo 9901 is a prime, and for a prime p :

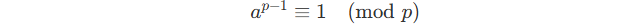
Directly divide LHS and RHS by a :

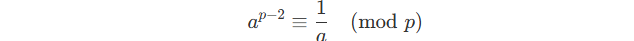
We get the inversion of a under modulo m .
Of course, you can also use other ways such as exgcd to get the same result, but these methods have theit own constraints, so use them properly.

Now, it\’s time to show WRONG code :

/*Failed.*/
#include <bits/stdc++.h>
using namespace std;
const long long MOD=9901;
long long LIM;
const long long SLIM=50000000;
bitset<SLIM+10> isprime, vis;
long long lprime[SLIM+11];

void preprocess() {
    lprime[1]=0;
    isprime[2]=1, vis[2]=1;
    lprime[2]=2;
    for (long long j=4;j<=LIM+10;j+=2) vis[j]=1, lprime[j]=2;
    for (long long i=3;i<=LIM+10;i++) {
        if (vis[i]) continue;
        lprime[i]=i, isprime[i]=1, vis[i]=1;
        for (long long j=i*i;j<=LIM+10;j+=i) vis[j]=1, lprime[j]=(lprime[j]?lprime[j]:i);
    }
}

long long qkpow(long long a, long long e) {
    if (e==0) return 1;
    if (e==1) return a%MOD;
    long long HF = qkpow(a, e/2);
    return (e&1?(a*(HF*HF)%MOD)%MOD:(HF*HF)%MOD);
}

int main() {

    long long a, b;cin >> a >> b;
    if (b==0) {
        cout << 1 << endl;
        exit(0);
    } 
    if (b==1) {
        cout << a << endl;
        exit(0);
    }
    LIM=a;
    preprocess();
    map<long long, long long> pfac;
    while (lprime[a]) {
        if (pfac.find(lprime[a])==pfac.end()) pfac[lprime[a]]=0;
        pfac[lprime[a]]++;
        a/=lprime[a];
    }
    long long fsum=1;
    //qkpow-inv del.
    for (map<long long, long long>::iterator it=pfac.begin();it!=pfac.end();it++) {
        long long pm=it->first, inv;
        inv = qkpow(pm-1, MOD-2);
        fsum *= (((qkpow(pm, it->second*b+1)+(MOD-1))%MOD)*inv)%MOD;
        fsum %= MOD;
    }
    cout << fsum;
    return 0;
}