21 Days Training // Day 6

T0. Fibonacci

Here, N \le 2 \times 10^9, if you directly compute F_i, the complexity is O(n), making you get a result of Time Limit Exceeded.
Then, how to solve it ?

If you watched the prev. page carefully, you can guess that this problem may need to use matrix.
But, how?
Think about this matrix :

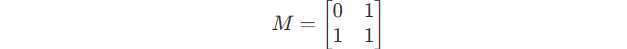
It also equals to :

If we compute M \times M, we can get :

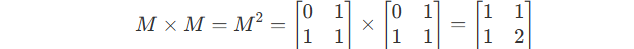
It also equals to :

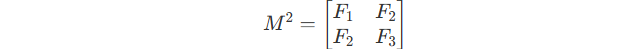
See it? It can \"naturally\" returns the reslut of F_3 .
Cannot believe it? More examples will show it.

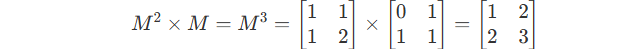
It also equals to :

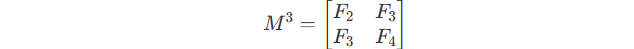
If you compute it many times, you will get the same results.
However, only examples cannot proof it right.
So we need to strictly proof it :

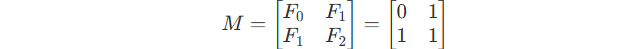
If we compute M^2 :

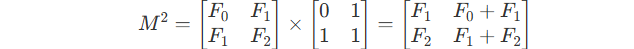
According to the fibonacci sequence\’s generation rule :

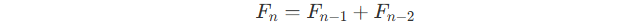
The product also equals to :

Now, suppose for positive integer N , this conclusion is right :

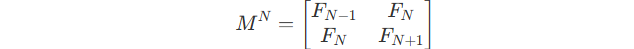
So we can get this equation :

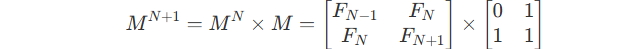
It also equals to :

Use the generation rule, we can get :

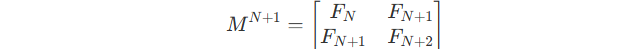
So, when the conclusion is right for N, it is also right for N+1 .
Since it is right for 1, it is naturally right for all positive integers.
Q.E.D.

But, it still cannot be used in this problem now……

Definitely Not !

You must remember this function :

int qkpow(int a, int e, int MOD) {
    if (e==0) return 1;
    if (e==1) return a%MOD;
    int p=qkpow(a, e/2);
    if (e%2==1) return (p*p*a)%MOD;
    return (p*p)%MOD;
}

Did you noticed something ?
We did not even restrict the type of a !
It only requires that 1, a, p are the same type and can be producted together (and mod).
So, if we let a equals to the matrix M, 1 equals to the matrix I …

Matrix UnitMatrix(long long K) {
    Matrix M0(K, K);
    for (long long i=0;i<K;i++) M0.change(i, i, 1);
    return M0;
};

Matrix qkMpow(Matrix Mx, long long e, long long MOD) {
    long long K = Mx.getHeight();
    if (e==0) return UnitMatrix(K);
    if (e==1) return Mx;
    Matrix HF = qkMpow(Mx, e/2, MOD);
    if (e&1) return ((HF*HF)*Mx)%MOD;
    return (HF*HF)%MOD;
};

We can compute the value of M^N with a complexity of O(\log n) !

Full Code :

#include 
using namespace std;
typedef vector V1D;
typedef vector V2D;

class Matrix {
    private:
        V2D value;
        long long MH, MW;
    public :
        // Matrix() {}
        Matrix(V2D Vec) {value=Vec;MH=Vec.size(), MW=Vec[0].size();}
        Matrix(long long H, long long W) {
            MH=H, MW=W;
            for (long long i=0;i<H;i++) value.push_back(V1D(W));
        }
        long long getHeight() {return MH;}
        long long getWidth() {return MW;}
        long long getValue(long long y, long long x) {return value[y][x];}
        void change(long long y, long long x, long long v) {value[y][x] = v;}
        V2D matrixVec() {return value;}
        Matrix operator+(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (Hx != MH || Wx != MW) {
                cout << "Matrix Exception (operator+, E1) : Size not equal.";
                exit(0);
            }
            Matrix Mr(MH, MW);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<MW;j++) Mr.change(i, j, value[i][j]+Mx.getValue(i, j));
            }
            return Mr;
        }
        Matrix operator-(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (Hx != MH || Wx != MW) {
                cout << "Matrix Exception (operator-, E2) : Size not equal.";
                exit(0);
            }
            Matrix Mr(MH, MW);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<MW;j++) Mr.change(i, j, value[i][j]-Mx.getValue(i, j));
            }
            return Mr;
        }
        Matrix operator*(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (MW!=Hx) {
                cout << "Matrix Exception (operator*, E3) : Illegal H/W.";
                exit(0);
            }
            Matrix Mr(MH, Wx);
            for (long long i=0;i<MH;i++) {
                for (long long j=0;j<Wx;j++) {
                    long long cur=0;
                    for (long long k=0;k MOD;
    Matrix M0(2, 2);
    M0.change(0, 1, 1);
    M0.change(1, 0, 1);
    M0.change(1, 1, 1);
    Matrix M = qkMpow(M0, N, MOD);
    V2D Vec = M.matrixVec();
    cout << Vec[1][0];

    return 0;
}

Now, you \"get a deeper understanding of\" the quick power of matrix, go to solve more problems!