21 Days Training // Day 6

T(-1). Matrix Product

Here are 2 matrixes, A and B.

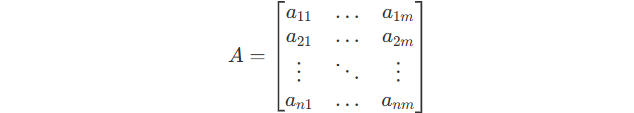
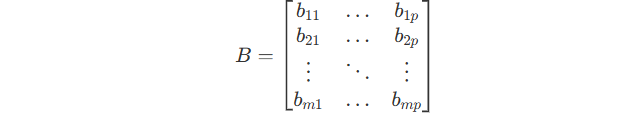
Their product be like :

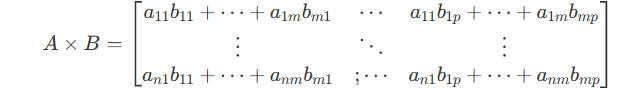
Or, for their product C = A \times B :

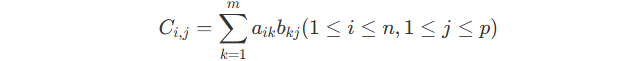
From this we can see that if 2 matrixes can be producted together, the 1st matrix\’s width is equal to the 2nd matrix\’s height.

To compute their product, this method\’s complexity is O(mnp) (not best optimized).

Properties :

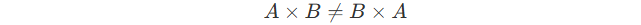
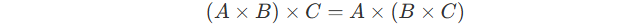
Inversion of A : the matrix P that satisfies :

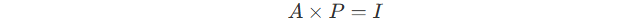
Here,

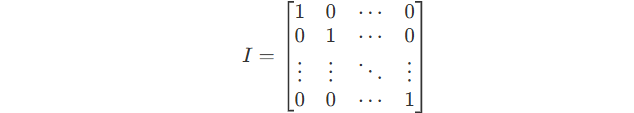
The size of I equals to A.

For some A , P may not exist.

Here are the simple algorithm to compute A \times B with complexity O(mnp) :

(The class Matrix also has operator+ and operator-)

#include 
using namespace std;
typedef vector V1D;
typedef vector V2D;

class Matrix {
    private:
        V2D value;
        long long MH, MW;
    public :
        // Matrix() {}
        Matrix(V2D Vec) {value=Vec;MH=Vec.size(), MW=Vec[0].size();}
        Matrix(long long H, long long W) {
            MH=H, MW=W;
            for (long long i=0;i<H;i++) value.push_back(V1D(W));
        }
        long long getHeight() {return MH;}
        long long getWidth() {return MW;}
        long long getValue(long long y, long long x) {return value[y][x];}
        void change(long long y, long long x, long long v) {value[y][x] = v;}
        V2D matrixVec() {return value;}
        Matrix operator*(Matrix Mx) {
            long long Hx=Mx.getHeight(), Wx=Mx.getWidth();
            if (MW!=Hx) {
                cout << "Matrix Exception (operator*, E3) : Illegal H/W.";
                exit(0);
            }
            Matrix Mr(MH, Wx);
            for (long long i=0;i M;
    V2D V1(N);
    for (int i=0;i V1[i][j];
    }
    int P;cin >> P;
    V2D V2(M);
    for (int i=0;i<M;i++) {
        V2[i] = V1D(P);
        for (int j=0;j
> V2[i][j];
    }
    Matrix M1(V1), M2(V2);
    Matrix M3=M1*M2;
    V2D V3=M3.matrixVec();
    for (int i=0;i<N;i++) {
        for (int j=0;j<P;j++) cout << V3[i][j] << ' ';
        cout << endl;
    }
    return 0;
}

Why we create such a complex operator ?
Because, through this way, we can solve problems faster.