1:李超线段树
2:二分图最大(权)匹配(匈牙利/KM),一般图最大匹配(带花树)
3:莫比乌斯反演

1.李超线段树

先让我们回忆一下该死的线段树,它常用来维护区间信息，可以在O(log N)的时间复杂度下实现单点修改、区间修改、区间查询(区间求和，求区间最大值，求区间最小值)等操作
那么李超线段树，它在线段树前面加了两个字，有什么不一样呢?——多了李超两个字(即答)

先看模板题洛谷P4097
题目要求维护这样的两个操作:
1.在平面上加入一条线段。记第 i 条被插入的线段的标号为 i，该线段的两个端点分别为 (x_0,y_0)和(x_1,y_1)。
2.给定一个数 k，询问与直线 x = k 相交的线段中，交点纵坐标最大的线段的编号（若有多条线段与查询直线的交点纵坐标都是最大的，则输出编号最小的线段）。特别地，若不存在线段与给定直线相交，输出 0

我们发现普通的线段树无法维护这样的东西，所以便有了李超线段树这个算法
李超线段树是一种用于维护平面直角坐标系内线段关系的数据结构

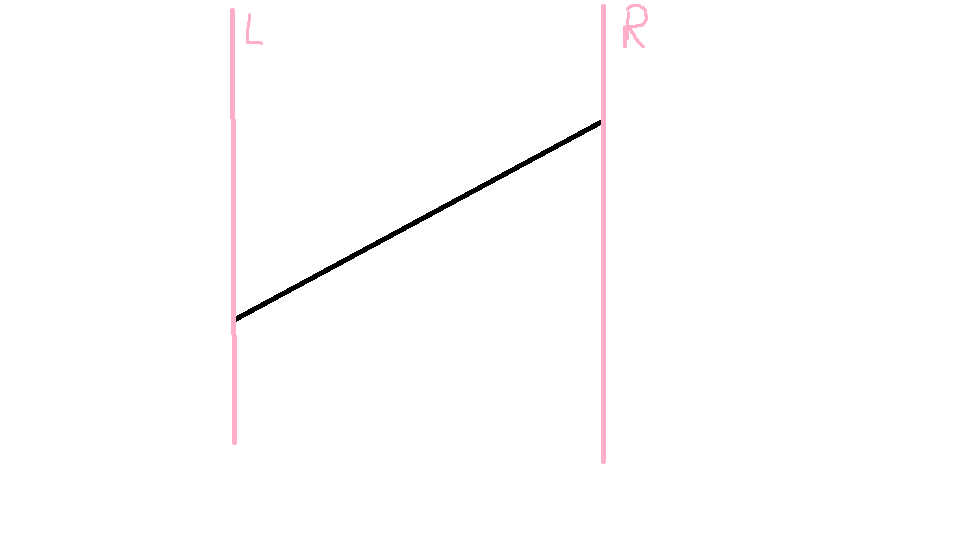
我们看上图，当只有一条线段时，显然他是最优解，那我们再加一条阁下又该如何应对

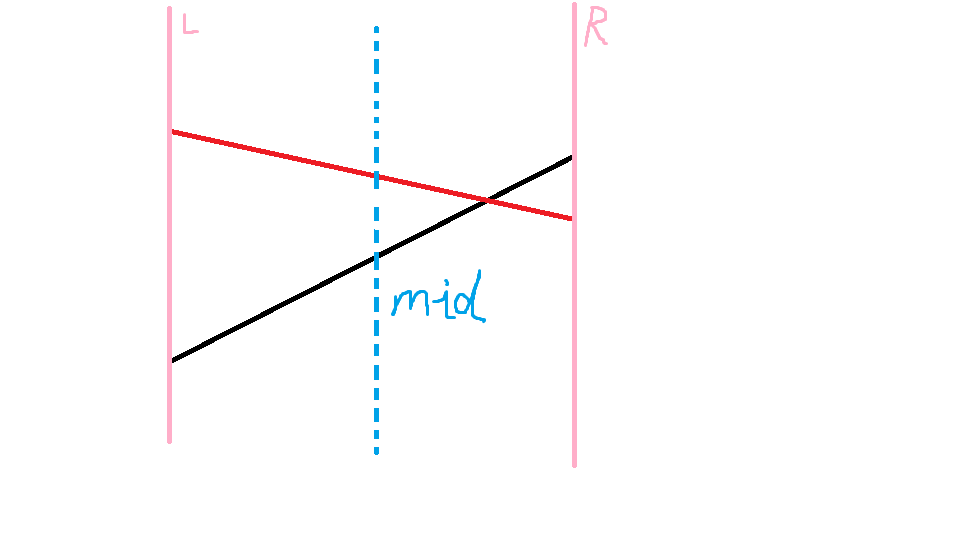
明显可以看出，插入新的线段(red)后，两条线段的交点左区间最优线段为新线段(red)，而交点右边区间最优线段则为原来的线段(blue)。扫一遍肯定来不及，所以我们二分递归求出所有区间的最优线段。
首先先取当前处理区间的 mid，如果新线段在 x=mid 时纵坐标更大，则先将当前区间的最优线段更替为新线段
那是否新线段(red)，就是最优解呢?显然是否定的，实际上交点右边的区间最优线段不是它，所以我们要两条线段再次进行比较，比较区间的左右两端点（即是判断区间内两条线段是否有交点，有交点说明要重新更新）。
如果被淘汰的线段(blue)在左右端点的比较中胜出，则将它继续递归，更新

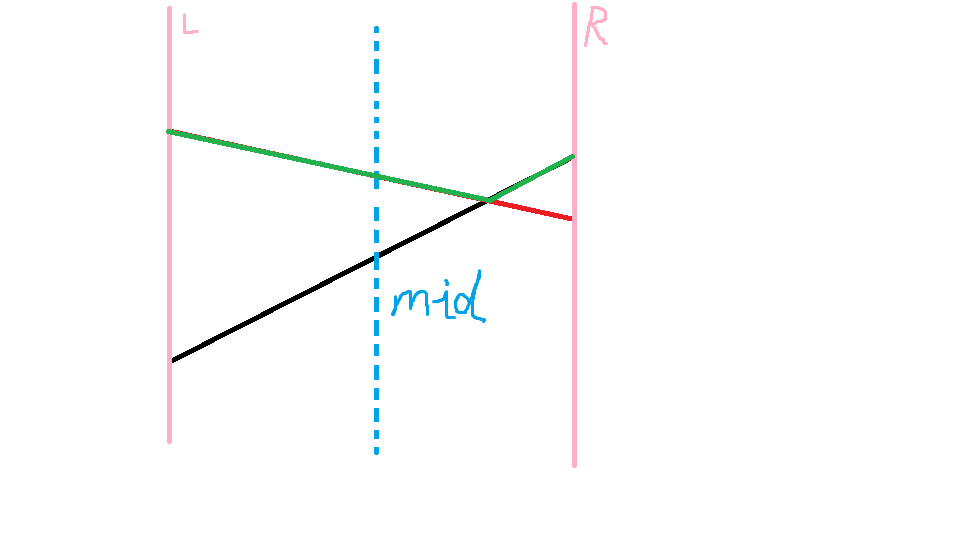
所以在最后我们得到了所有区间的最优线段(green)
询问的时候单点询问，递归取 max 即可
(模板题代码就不放了，自己找适合的，名字里带线段树的算法的代码就是长)

我还打了这个洛谷P4254
其实一个意思，只要改一下输入就好

2.二分图最大(权)匹配(匈牙利/KM),一般图最大匹配(带花树)

我能说我看不懂吗？,这里的老师说这放省选都冷门，我都没去听，他说匈牙利是前置知识，但我不会，那我还听个啥

3.莫比乌斯反演

数学知识超纲了哈，不会