七月的Last Day
今天没比赛,讲专题
早上讲李超线段树,听不懂一点,大致是用于求解在平面内给定线段中,对于一个x值其对应的最大y值是多少的数据结构,是线段树的一个变种
由于实在搞不懂,于是我就只好自学点其它东西了
Johnson算法
这是一种用于求解全源最短路的算法,其本质思想就是跑次dijkstra或bellman-ford(spfa),神奇的是,这玩意对于求有负权边的图时,也可以考虑用dijkstra算法,不过要用spfa预处理一下负权边
在学这个到时候,我第一次听说图论中有势能这一概念
具体内容看
模板题
luogu B3609
Code
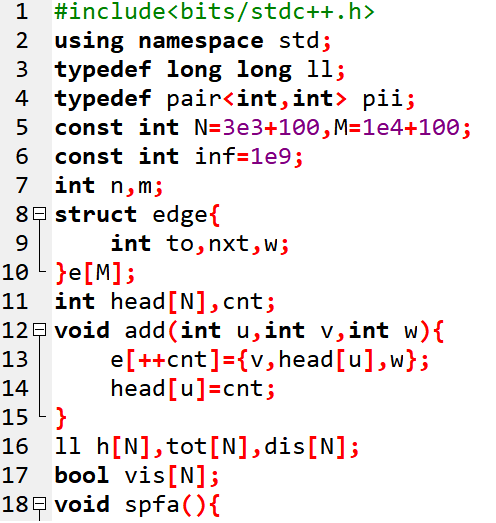

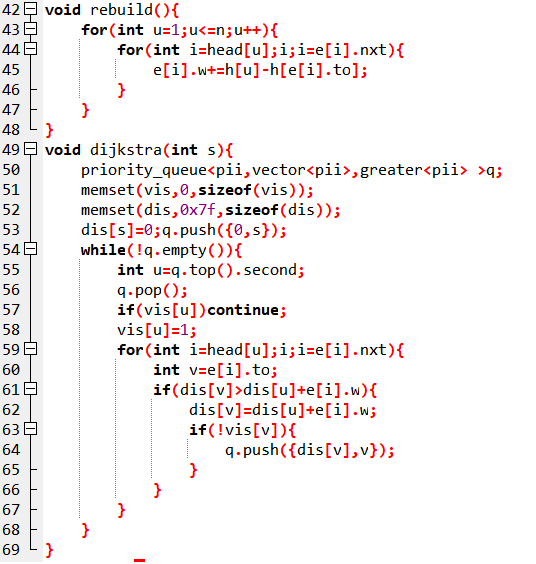
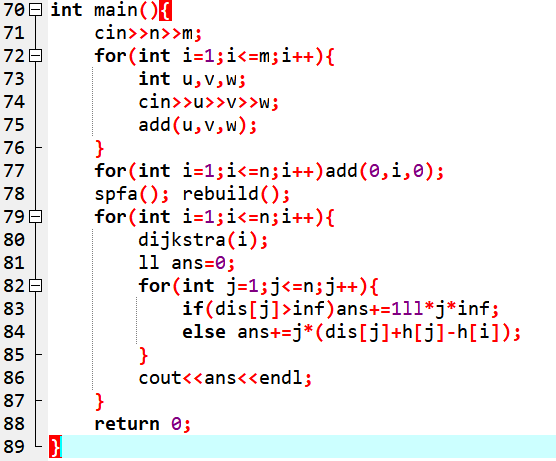
首先用spfa处理图中的负权边,建立超级源点后,将其到各点的最短距离作为各点的势能,并同时判断是否有负环
接着用各点的的势能重构图中边权后,就能跑dijkstra了,这里用的是其堆优化版本
数论题
T1 因子和Luogu P1593
这题刚看题目就知道应该要用质因数分解了,但是分解完后就不知道要怎么做了
看了题解,得到了一个比较重要的公式
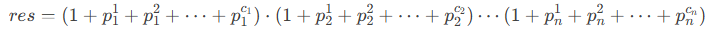
这是经质因数分解后,求解因子和的公式
有了这个以后,再用等比数列求和公式化简,用快速幂求解
但是会发现,求解时要除以一个(pi-1)的项,那么由于是在模意义下的,我们可以看作乘上(pi-1)关于9901的乘法逆元
若gcd(pi-1,9901)=1那么就存在乘法逆元,又注意到9901是质数,因此我们可以用费马小定理求解乘法逆元;若不是,则说明pi-1应为9901的倍数,那么就很好处理了
于是 (pi-1) mod 9901 = 0
则pi mod 9901 = 1
所以对于上面乘积式的该分量,就等于其最大幂数+1
Code:

细节注意:最后的答案输出先加了M再模M后输出答案的原因是前面sum函数中第二个return中有一个(quick_pow(x,y+1)-1)的项,这项有可能为负数,因此需要处理
T2 签到题Luogu P3601
不是我嘲讽它的难度,是这题真的叫做签到题,但是难度达到了蓝题的水准,没看题解自己做真做不动,事实上题目翻译一下就是要我们求这样一个东西
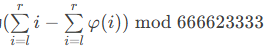
不难发现左边的求和O(1)就能搞定,但是右边的这个和它的数据范围,真的一言难尽,
题解的思路也是非常巧妙,模仿了筛法的思想,将1e6范围内的质数预处理出来,再考虑其倍数的欧拉函数值,利用欧拉函数是积性函数的性质,进行求解,另外就是可以把下表减掉一个L,这样数组就放得下了
一篇比较好的题解
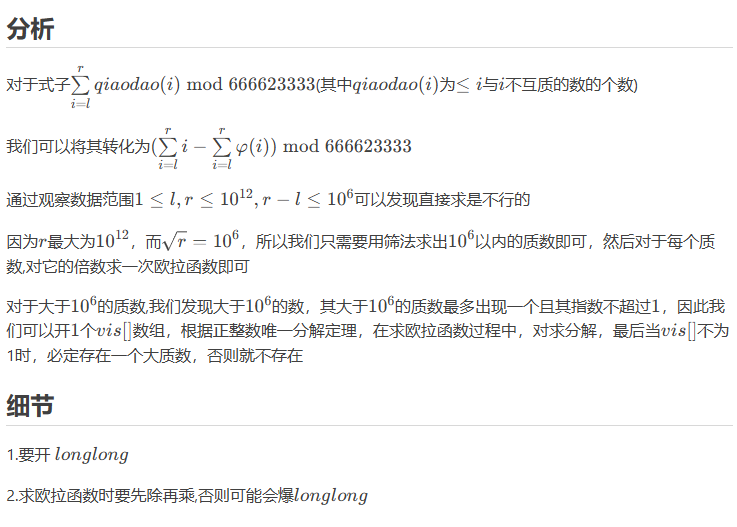
其中求解欧拉函数我们要用到的公式

这不得记下
然后就是Code了

细节:除了题解当中的,我认为比较巧妙的就是主函数第二个循环中,用下标取余找倍数的部分,这里一定要对pi再取余一次,因为可能会出现刚好L是pi的倍数,那么应该从j=0开始枚举,如果没有再取余的话,就会从j=pi开始枚举,就会漏掉j=0的情况
T3及其加强版
题意大致就是给定一个n,然后求对于1~n每个数的约数个数之和
这两题简直天壤之别,一道普及-,另一道直接变黑题了
先讲讲弱版的解法吧
P1403
这个事实上我们可以用逆向思维来解决,原题等价于求1到n中1到n的倍数个数之和(这么表达好像有点奇怪,但无伤大雅),那就十分简单了,答案就是
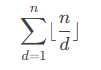
代码也很简短,没有几行

SP26073
话锋一转,来看看黑题的数据规模

n这么大也就算了,还多测,很难想象时间复杂度的式子长什么样,直接看题解吧
哇塞,这个题解第一步转换就很离谱

说实话看得不是很懂,AI说可以拆开证明,但能想到这个式子也是注意力惊人
然后题解说需要用到Stern–Brocot,我听都没听过,又去OI_WIKI上恶补了一会,发现根本看不懂
于是这题就先放着了,下次再打(君子报仇,十年不晚bushi)