21 Days Trainging // Day 5

2. quiz

My idea :

1. For query 1, directly change each character.
2. For query 2, use dp to get the answer.
3. Here dp[i][j] = current count, i = current pos in substr, j = divides remain.
4. Notice that each block can only have 4 character at most, so we can get dp][i][j] from dp[i-1,…,i-4][j-1].
5. Enumrate i-1,…,i-4, and stop at these conditions :
   • When next pos is smaller than 0.
   • When current block is not strictly increasing.
6. Initialization
   • For dp[i][0], check if the current block is strictly increasing.
   • For dp[i][i], this formula equals to 1.
   • For dp[i][j](j>i), this formula equals to 0.

Not std BF code :

#include 
using namespace std;

vector<vector > dp;
int main() {
    freopen("quiz.in", "r", stdin);
    freopen("quiz.out", "w", stdout);
    string S;long long L, opt;
    cin >> L >> opt >> S;
    for (long long i=0;i> type ;
        if (type==1) {
            long long L, R;cin >> L >> R;
            for (long long i=L-1;i> L >> R >> k;
            long long Lx = R-L+1;
            if (k>Lx) {
                cout << 0 << endl;
                continue;
            }
            string T=S.substr(L-1, Lx);
            dp.clear();
            for (long long i=0;i<Lx;i++) {
                dp.push_back(vector(k));
            }
            for (long long i=0;i<Lx;i++) {
                for (long long j=0;ji) dp[i][j]=0;
                }
            }
            for (long long i=1;i3) dp[i][0]=0;
                else {
                    for (long long p=1;p<=i;p++) {
                        if (T[p]<=T[p-1]) goto j0_check_end;
                    }
                }
                dp[i][0] = 1;
                j0_check_end: ;
                for (long long j=1;j<=min(k-1, i);j++) {
                    dp[i][j]=0;
                    char mic='E';
                    bool stat=1;
                    for (long long p=1;p=mic) stat=0;
                        if (stat) {
                            mic=T[i-p+1];
                            dp[i][j] += dp[i-p][j-1];
                            dp[i][j] %= 998244353;
                        }
                    }
                }
            }
            cout << dp[Lx-1][k-1] << endl;

        }
    }
    return 0;
}

Constraints :

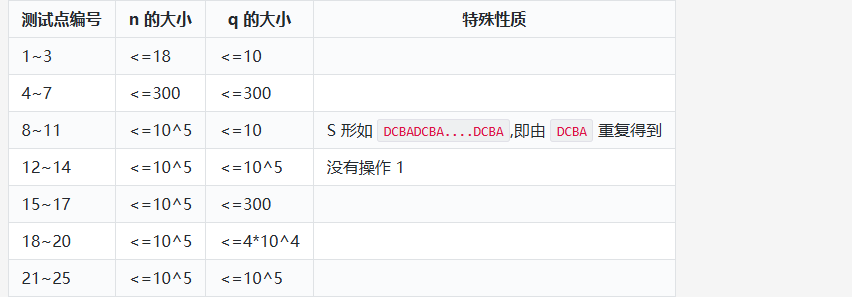
Expected : 12/12