早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
打比赛—-2025.07.30【提高B组】模拟赛
今天少了150分!!!
传送门
T1(20 -> 100)
题目描述
法师 M·拉斯莫迪斯在煤矿森林的塔楼上研究灵界,他精通许多
元素语言。探访星露谷社区中心后,你想要学习祝尼魔的文字,于
是前往煤矿森林向法师大人求助.法师大人想要锻炼你了解大自然
的程度,于是提议和你玩一场游戏。
法师塔的门口有一颗古树,法师和你将轮流使用森林的魔法来进
行游戏,法师先进行操作。具体而言,如果把古树当成一颗有n个
节点的无根树,每次森林魔法可以选择两个相邻的节点 (u,v),并
使得古树上所有连接 u 的无向边重新连接到节点v而不是 u。简
单来说,对于每条边(u,w)在操作后会变为(v,w),其中w不等于v.
不过这样可能会使游戏永远停不下来,这样你就没有时间给地里
的防风草浇水了。因此法师添加了一条规则:操作前后的树不能同
构。具体而言,设V(S),V(T)分别为树S和T的顶点集,存在双射f:
V(S)→V(T) ,使得 u,v 之间在树 S 里有边当且仅当使得 f(u),
f(v) 之间在树 T 里有边。
当一个人无法进行有效操作时,另一个人获胜。假设你和法师都
采用最佳策略,你想知道谁能使用森林魔法取得最终胜利?
输入
第一行输入T 表示有多少组测试数据;
接下来每组数据第一行n(2≤n≤50),表示古树的节点数量。随后
n−1 行,每行输入两个正整数 u, v,表示树上有 u,v 这条无向
边。保证输入的边能构成一颗树。
输出
对于每组数据,若法师获胜,输出一行 wizard;若你获胜,输
出 villager;若游戏永远不会结束,输出 never ends。输出对
于大小写敏感,建议直接复制这里的文本。
赛时思路:
找样例的规律,得了20分
时间复杂度 O(n)
赛时代码:

标程思路:
由于树的节点数至少是 2,每个点的度数至少是 1,称度数为 1 的点为“叶子”。
可以观察到将和 u 相连的边(除了 uv ) 都接到 v 上时:
1.如果u是叶子,那么没有边发生改变,此时操作后的树和操作前的树同构;
2.如果v是叶子,那么把相当于只交换了u和v的标号,此时操作后的树仍然和操作前的树同构;
3.否则u会成为新的叶子,v的度数得变大,其他点的度数不发生改变,此时叶子数量恰好增加了1,因此操作后的树必然和操作前的树不同构。
因此只要统计输入的树上,有多少条边两侧都不是叶子,只有操作这种边不会导致同构,因此这就是总共能操作的次数。根据能操作的次数奇偶性判断谁赢即可。
时间复杂度 O(n)
标程代码:

T2(0(36) -> 36)
题目描述
丰富的美食让你们心满意足,肚子饱饱的你准备下井探矿,寻
找星露谷失落的珍宝。
每个矿井间通过错综复杂的隧道连接,而且还受到结界的影响.
具体而言,矿井和隧道呈现为一张有向带权图,其中权值是通过该
隧道的时间。由于里面时常有怪物出没,经过前人的探索,每条隧
道被设立了魔法结界,为了保障安全都只有一个方向是可以通过,
即这是一张有向图。
不过森林的魔法波动让隧道结界发生了变化。第 0 天,隧道没
有变化,而在第 1∼m 天的凌晨,若第 i 天的波动值 p i 为 1,
则第 i 条隧道的结界方向会发生变化,直至午夜时恢复原结界方
向,即这条边会反向,一天后恢复。若 p i 为 0 则表示该隧道
结界足够强大,未受到波动影响。
假设起点在矿井 S=1号矿井,珍宝的位置在矿井 T=2号矿井,
你想知道如果你中午进入起点,从 S 到达 T 的最短时间相比于
魔法波动前(即相比于第 0 天),会变大、变小还是不变?保证
第0天两者联通。
输入
第一行输入两个数 n,m ,表示矿井和隧道的数量;
接下来输入一行一个长度为m的字符串p,其中p i表示第i天隧
道 i 是否受到波动影响。
最后 m 行每行输入三个数 u i,v i,w i (1≤u i,v i≤n,1≤c i
≤10^5),表示这条隧道的起点、终点、通过时间。
输出
第一行先输出第 0 天从起点到珍宝的最短时间。
接下来 2∼m+1 行:
若今天从起点到珍宝的最短时间变小了,输出 HAPPY;
若今天从起点到珍宝的最短时间变大了,输出 SAD;
若今天从起点到珍宝的最短时间未变,输出 SOSO;
赛时思路:
对于每一个改变,用Dijkstra暴力求解即可
时间复杂度 O((V+E)\log V)
赛时代码:
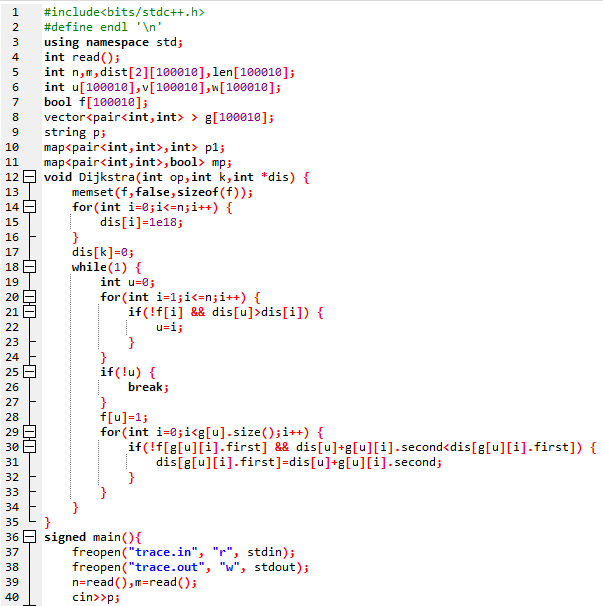
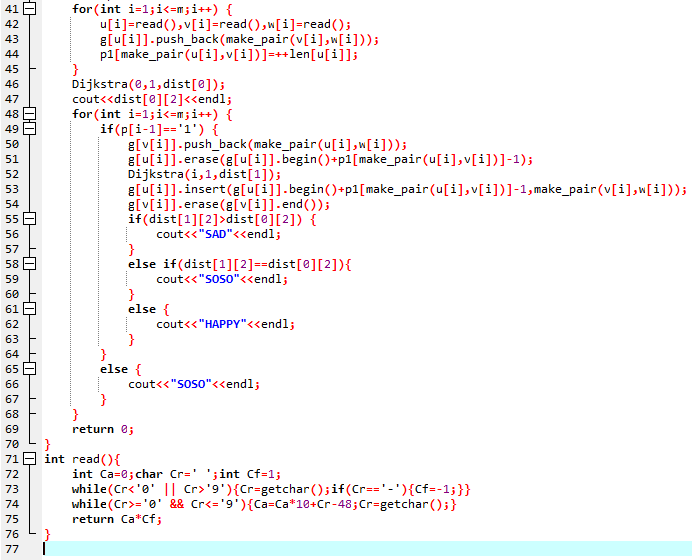
标程思路:
先求出最短路,之后先根据最短路判断是否变小,最后用tarjan求强联通分量求出从s到t的桥边,即可判断是否会变大。
具体来说,先找出一条s到t的链,之后用拓扑排序统计每个点通过非链边最远能到多远,设该点在H上深度为x,最远能到maxd,那么x+1~maxd这些链边都不是桥边。
时间复杂度 O(n\log n)
标程代码:
没打,就不放了
T3(12 -> 56)
题目描述
你刚从矿井深处归来,背包里满是水晶碎片与稀有宝石。天色
将晚,莉亚在河边画画,镇上格斯的酒馆已经灯火通明。
当你路过博物馆时,图书馆馆长古纳给了你一张尘封的纸卷:"
这是我在整理档案时发现的旧卷轴,据说是早期探险者留下的逻
辑谜题。你愿意试试吗?”
你展开卷轴,只见上面写着若干个不定项选择题。在你思考良
久后,馆长不忍心看你冥思苦想,告诉了你卷轴上试题的答案.
可是你念出答案后受到了魔法的反噬,瞬间晕了过去。
第二天,你的脑子里只剩下了一串由 A, B, C, D 组成的字
符串,你非常好奇自己获得的秘密,但是馆长可不会轻易让你获
得卷轴的秘密,他给出了 q 个操作来考验你。
具体来说:
一道不定项选择题的答案是由 A, B, C, D 中按照字典序排
列形成的非空字符串。首先,这意味着一道不定项选择题至少包
含一个正确选项;其次,比如 ABD, C, AD 可以是一道不定向
选择题的答案,但是 DA, BB,空串不能是一道不定项选择题的
答案;
一份卷轴上的试题,指的是若干道不定项选择题的答案连接成
的字符串,其中包含的不定项选择题题数不一定确定。比如试题
ABDACD 可以是由 AB, D, ACD 这三道选择题组成的字符串,也
可以是由 A, BD, A, CD 这四道选择题组成的字符串;试题上,
每个选择题的题号从 1 开始编号,两份试题不同当且仅当题号
相同的选择题答案不同;
梦醒时分,你脑子里只记得梦里一个长度为 n 的由 ABCD四
个英文字母构成的字符串 S。图书馆馆长会给出 q 次以下两种
操作:
1.给出 l, r,对于 l≤x≤r,将 S x变为下一个选项,即
A 变为 B,B 变为 C,C 变为 D,D 变为 A。
2.给出 l, r, k,对于 S l,S l+1,...,S r依次连接得
到的答案字符串,求出有多少份恰好包含 k 道不定项选择题的
不同试题,其答案恰为这个字符串。由于答案可能过大,输出
对 998 244 353 取模后的结果。
图书馆长说假如你通过他的考验,就把古老卷轴的完整秘密告
诉你,你能回答他的问题吗?
输入
第一行,两个整数 n,q(1≤n≤10^5,1≤q≤10^5),表示你梦里
字符串的长度,以及馆长给出的操作次数。
第二行,长度为 n 的字符串 S,表示你梦里的答案字符串。
接下来 q 行,每行第一个整数 op(1≤op≤2),表示图书馆
长给出第 op 种操作。当op=1时,之后包含两个整数 l,r(1
≤l≤r≤n),表示操作参数。当op=2时,之后包含三个整数l,r,
k(1≤l≤r≤n,1≤k≤n,不保证 k∈[1,r−l+1],表示操作参数。
输出
对于第二个操作,输出一行一个整数,表示所求的答案对 9982
44353 取模的结果。
赛时思路:
隔板法+暴力+O(n)求组合数
时间复杂度 O(nm)
注意要判断组合数中的a,b大于0
我就是因为这个少了44分
赛时代码:

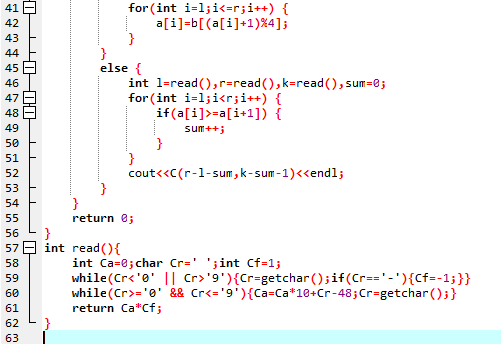
标程思路:
测试点1~7
暴力dp即可
测试点8~11
可以发现DCBADCBA…中,只有AD中间的位置可以有变动的空间、能够成为1或2道选择题。其他C、B都必须单独成为一道题,不然不符合上升条件。那么统计好不能连起来的位置由多少、能动的位置有多少,即成为隔板法。
设不能连起来的(隔板的)数量是c,那么答案即为 C(k-l-c,r-l-c)
q只有10,暴力维护即可。
测试点12~17
分析上面一栏测试点,可以发现我们只需要统计“不能连起来的、强制成为隔板的位置”有多少个即可。考虑 S[l,r] 中相邻的两个字符,如果 ,那么 与 不可能为同一道题的答案,因此二者之间必须放置隔板。不妨将这些隔板的数量记作 c。假设你不会滚动操作,可以强行统计并用前缀和得出c,最后用隔板法得出答案。
测试点18~20
使用线段树或分块等数据结构,维护当前区间平移了多少次。平移后,内部的隔板数量不会变化,只有左右端点会产生变化。对相邻区间进行单点查询即可。
时间复杂度 O(n \log n)
标程代码:
没打,就不放了
T4(0(70) -> 100)
题目描述
了解了祝尼魔的语言后,你得知祝尼魔想要尝各类星露谷美食.
每天,美食节目酱料女王都会在电视上播出。可是女王不会轻
易让大家学会自己的美食配方,因此她将食谱隐藏在了两串由小
写英文字母构成的咒语S和T中。从咒语 S 中选出一个连续子串
p,从咒语T中选出一个连续子串q,若p和q拼起来是一段“平方咒
语”,则可以参悟一道食谱的配方。“平方咒语”的意思是,这个
拼接后的字符串由一个字符串重复两次得到,如 abcabc,star
villagestarvillage。而如 aabbaa 则不是。
由于咒语跟时间顺序息息相关,所以只要选出 p 和 q 的位置
不同,就算作一道不同的新菜谱。比如S=abab, T=ab, 选取p 1
=S[1:2]=ab 和 p 2 =S[3:4] 都能与 q=T[1:2]=ab 拼出平
方咒语 abab, 但是由于 p 是从不同位置选出的,咒语受到了时
间变化的影响,因此也算作两道不同的美食食谱。
祝尼魔想要品尝尽可能多的美食,他们想知道,今天的酱料女
王节目中,最多可以学到多少道菜谱?
输入
第一行输入咒语S,第二行输入咒语T,保证长度小于等于 5000。
输出
对于每组数据,输出最多能学到多少道菜谱。
赛时思路:
- 对于测试点 1 ~ 5,处理出 S 的所有的可能的连续子集和 T 的所有的可能的连续子集,在 S 的所有的可能的连续子集和 T 的所有的可能的连续子集中各取一个,拼接,判断是否合法,统计个数即可
时间复杂度 O(n^6),分数:25 分 - 对于测试点 6 ~ 8,不妨设 S=k_{1} 个 a+1 个 b+k_{2} 个 a,T 的长度为 len,m 为不超过 len 的最大奇数。
首先先考虑在 S 中只取 b 的情况,容易发现答案即为 \sum\limits_{i=1;i \equiv 1 \pmod{2}}\limits^{m}{(len-i+1)}
再考虑在 S 中取若干个 a 和一个 b 的情况,容易发现答案即为 min(k_{1},k_{2}) \times len
所以 ans=\sum\limits_{i=1;i \equiv 1 \pmod{2}}\limits^{m}{(len-i+1)}+min(k_{1},k_{2}) \times len
时间复杂度 O(n),分数:15 分 - 对于测试点 9 ~ 13,不妨设 S=k_{1} 个 a+k_{2} 个 b+k_{3} 个 a,S 的长度为 len_{S},T 的长度为 len_{T}
依然先考虑在 S 中只取 b 的情况,容易发现答案即为 \sum\limits_{i=1}\limits^{k_{2}}{\sum\limits_{j=1;i+j \equiv 0 \pmod{2}}\limits^{len_{T}}{(len_{S}-i+1) \times (len_{T}-j+1)}}
再考虑在 S 中取若干个 a 和若干个 b 的情况,观察可得到这 k_{2} 个 b 必须都取,才有合法的情况,即答案为 min(k_{1},k_{3}) \times (len_{T}-k_{2}+1)
所以 ans=\sum\limits_{i=1}\limits^{k_{2}}{\sum\limits_{j=1;i+j \equiv 0 \pmod{2}}\limits^{len_{T}}{(len_{S}-i+1) \times (len_{T}-j+1)}}\\ + min(k_{1},k_{3}) \times (len_{T}-k_{2}+1)
时间复杂度 O(n^2),分数:25 分。这里其实可以优化成 O(n),但 n^2 也能过
综上,理论得分为 65 分
注意到在题目的下发文件中有一个数据点,输出答案1061574,5分
所以理论得分应为 70 分
但由于测评网站的空间限制过于离谱,所以爆 0 了
赛时代码:
图片
标程思路:


标程代码:
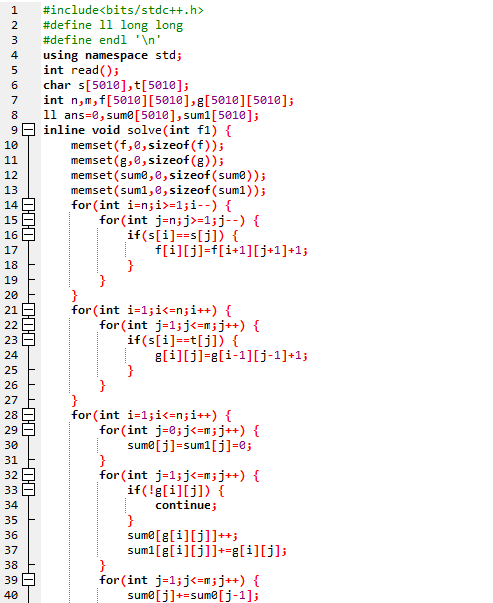

下午
改题目
晚上
打博客
博客从6:00打到了9:15