早上比赛
今天又是模拟赛,这次竟然打了140多分,十分意外。但是很可惜,看T1的时候以为很难,需要换根操作之类的,结果只是一道很简单的找规律题,在比赛结束前几分钟草草凭感觉蒙了几个性质上去,拿了65,本来应该可以AC的。后面的T4性质二的分没拿到,原因是忘了把修改后的代码复制上去了(新开一个文件调试代码的坏处)。还有就是打T2的时候,本来说没有重边与自环的,结果样例里边又出现了重边,给我干蒙了,我在那里调了好久的dijkstra,不过倒也提醒了我反转后可能有重边,修改了一下,把暴力分和pi=0的性质的分拿了。总之,又是暴力骗分的一天
T1 森林魔法
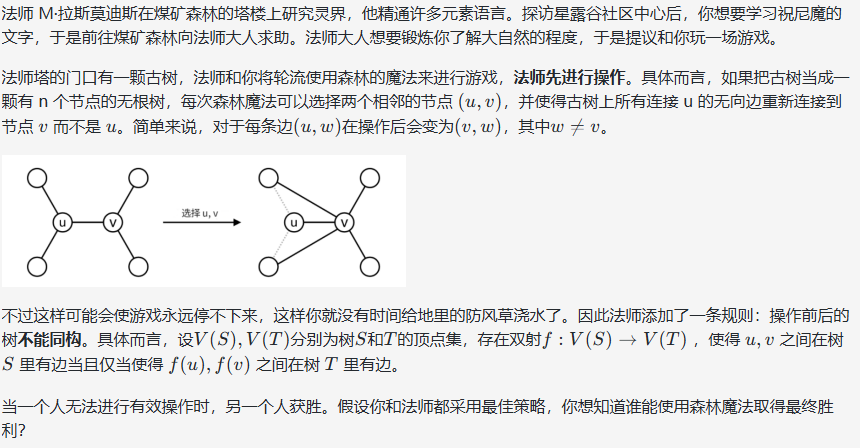
这题的样例也很人性化,手模一下就能发现很多小性质,比如说对于链的情况,不难发现,当链的边数为奇数时,法师赢,反之,则我赢;又或是对于出现有一个点度数为n-1时,显然我赢……但这都不是重点,再多模拟几次就能发现,事实上,对于树来说,其可操作数即为n-1-叶节点个数,这样一来只需统计叶节点个数,再利用奇偶性,就能得到答案
要实现统计叶节点的个数也很简单,只需记录有多少个度数为1的顶点个数即可
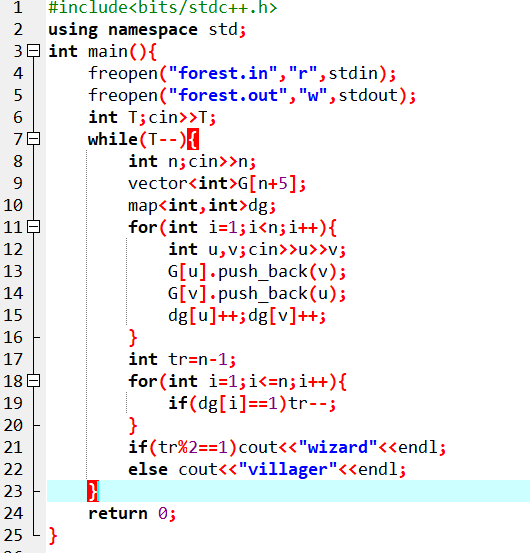
这里的建图都多余了
T2 矿井寻踪
题目描述
丰富的美食让你们心满意足,肚子饱饱的你准备下井探矿,寻找星露谷失落的珍宝。
每个矿井间通过错综复杂的隧道连接,而且还受到结界的影响。具体而言,矿井和隧道呈现为一张有向带权图,其中权值是通过该隧道的时间。由于里面时常有怪物出没,经过前人的探索,每条隧道被设立了魔法结界,为了保障安全都只有一个方向是可以通过,即这是一张有向图。
不过森林的魔法波动让隧道结界发生了变化。第0天,隧道没有变化,而在第 1∼m 天的凌晨,若第 i 天的波动值pi为1,则第 i 条隧道的结界方向会发生变化,直至午夜时恢复原结界方向,即这条边会反向,一天后恢复。若pi为0则表示该隧道结界足够强大,未受到波动影响。
假设起点在矿井S=1号矿井,珍宝的位置在矿井T=2号矿井,你想知道如果你中午进入起点,从S到达T的最短时间相比于魔法波动前(即相比于第 0 天)会变大、变小还是不变?保证第0天两者联通。
赛事思路
先看性质

注意到dijkstra堆优化的复杂度是O(nlogn)的,所以暴力跑的话,总复杂度就是
O(mnlogn),事实上会更小,因为是稀疏图,可以AC掉前1~7个点
又不难想到,对于pi=0,既没有边反向的话,是和之前的答案一样的,直接输出SOSO即可,这样可以拿到44分
正解
先用dijkstra跑一遍,得到1到其它顶点的最短距离,再用反图跑一遍dijkstra,得到2到其他顶点的最短距离
对于边e(u,v,w)来说,被反向后,若从1到2的最短距离d变小,必然是这条边在新的最短路上,因此有dis(1,v)+dis(2,u)+w<dis(1,2)
若不然,考虑到对于从1到2的最短路径来说,可能有很多条,但这些最短路径组成的图是一个DAG,我们判断e是否为这个DAG上的桥,若是,则必然最短路径边长;反之,则不变。
这样的话,我们用tarjan算法预处理后,判断一下e是否为DAG上的桥即可
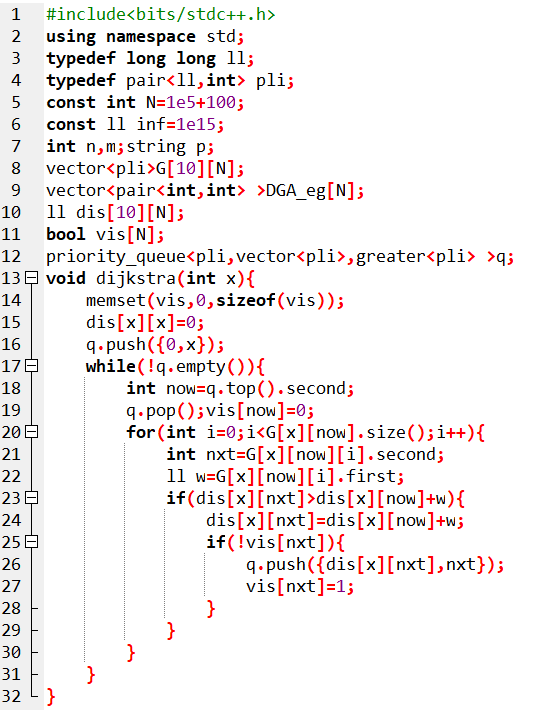


温馨提示,注意第87行的后两个判断是一定要加的,因为可能两个距离加起来以后,越界了,变负数,导致答案错误
附:割点和桥(Tarjan算法)
概念详见OI Wiki 割点与桥
这里主要复习用Tarjan算法判断割点和桥(回忆常州集训那些日子ing)
Tarjan——割点

Tarjan——桥
前面有了,这里就不打了
防遗忘
最后再附上一篇好文
Link