早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
打比赛—-2025.07.29【提高B组】模拟赛
传送门
T1(40 -> 40)
题目描述
小菜的妹妹小诗就要读小学了!正所谓计算机要从娃娃抓起,
小菜决定在幼儿园最后一段轻松的时间里教妹妹编程。
小菜刚教完gcd即最大公约数以后,一知半解的妹妹写了如
下一段代码:
sum:=0;
for i:=1 to n-1 do
for j:=i+1 to n do sum:=sum+gcd(i,j)
显然这个程序的效率是很低的,小明打算写一个更强的程序,
在求出sum的同时比妹妹跑的更快。
输入
第一行一个整数t,即表示有t组数据
接下来t行,每行一个整数n
输出
t行,每行一个整数,表示n所对应的sum值
赛时思路:
设 f_i 表示 n 所对应的 sum 值,则 f_i=f_{i-1}+\sum\limits_{j=1}\limits^{i-1}{gcd(i,j)}
n^2 预处理即可
时间复杂度 O(n^2)
赛时代码:

标程思路:
我们要求的式子:\sum_{i = 1}^{n – 1} \sum_{j = i + 1}^{n} \gcd(i, j)
现在我们逐步化简: \begin{aligned} \sum_{i = 1}^{n – 1} \sum_{j = i + 1}^{n} \gcd(i, j) &= \sum_{i = 1}^{n} \sum_{j = i + 1}^{n} \gcd(i, j) \\ &= \sum_{j = 1}^{n} \sum_{i = 1}^{j – 1} \gcd(i, j) \\ &= \sum_{d = 1}^{n} d \times \sum_{j = 1}^{n} \sum_{i = 1}^{j – 1} [\gcd(i, j) = d] \\ &= \sum_{d = 1}^{n} d \times \sum_{j = 1}^{\left\lfloor \frac{n}{d} \right\rfloor} \sum_{i = 1}^{j – 1} [\gcd(i, j) = 1] \\ &= \sum_{d = 1}^{n} d \times \sum_{j = 1}^{\left\lfloor \frac{n}{d} \right\rfloor} \varphi(j)\end{aligned}
(注意本题的特殊性,我们需要重新定义 \varphi(1)=0 )
时间复杂度 O(n+Tn\sqrt{n})
这显然会超时,所以用到分块操作
令 sumphi(x)=\sum\limits_{j=1}\limits^{x}{\varphi(j)}
和 sum(x)=\sum\limits_{j=1}\limits^{x}{j}
那么原式就可以化为: \sum\limits_{d=1}\limits^{n}{d} \times sumphi(\left\lfloor \frac{n}{d} \right\rfloor)
可以发现,我们枚举了很多 d ,使得很多 \left\lfloor\frac{n}{d}\right\rfloor 都相等,所以我们可以把 \sum\limits_{d=1}\limits^{n} ,分成 \sqrt{n} 块,使得每一块的 \left\lfloor\frac{n}{d}\right\rfloor 都相等,这样我们可以通过结合律得到下面的式子,预处理 sumphi(x),sum(x) ,来简化时间复杂度到 O(n + T\sqrt{n})
故 ans = \sum\limits_{l=1}\limits^{n}{(sum(l)-sum(l-1)) \times sumphi(\left\lfloor \frac{n}{l} \right\rfloor)}
标程代码:
没打,就不放了
T2(24 -> 80)
题目描述
农民 John 购买了一处肥沃的矩形牧场,分成 M * N 个格
子。他想在那里的一些格子中种植美味的玉米。遗憾的是,有
些格子区域的土地是贫瘠的,不能耕种。精明的 FJ 知道奶牛
们进食时不喜欢和别的牛相邻,所以一旦在一个格子中种植玉
米,那么他就不会在相邻的格子中种植,即没有两个被选中的
格子拥有公共边。他还没有最终确定哪些格子要选择种植玉米。
输入
第一行两个用空格分隔的整数 M 和 N
第二到第 M+1 行,第 i+1 行描述牧场第i行每个格子的
情况, N 个用空格分隔的整数,表示 这个格子是否可以种
植(1 表示肥沃的、适合种植,0 表示贫瘠的、不可种植)
输出
一个整数: FJ 可选择的方案总数 除以 100,000,000
的余数。
赛时思路:
将二维矩阵 A 转化为一维数组 B ,其中 A_{i,j}=B_{(i-1)*m+j}
再 2^{n \times m} 的枚举所有的可能,并判断是否合法,统计数量即可
时间复杂度 O(nm2^{n \times m})
赛时代码:
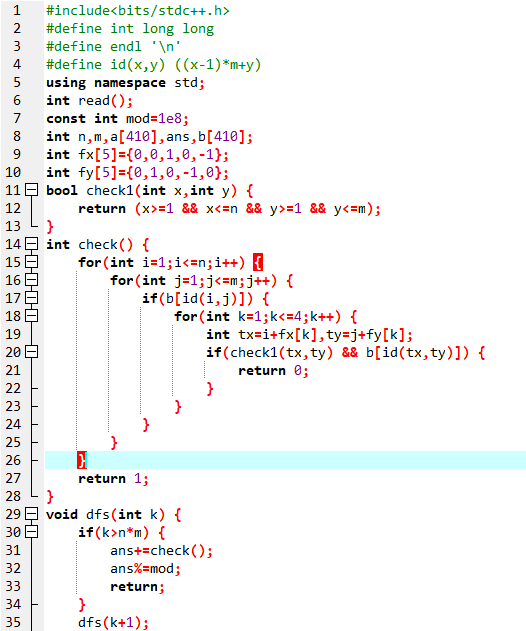
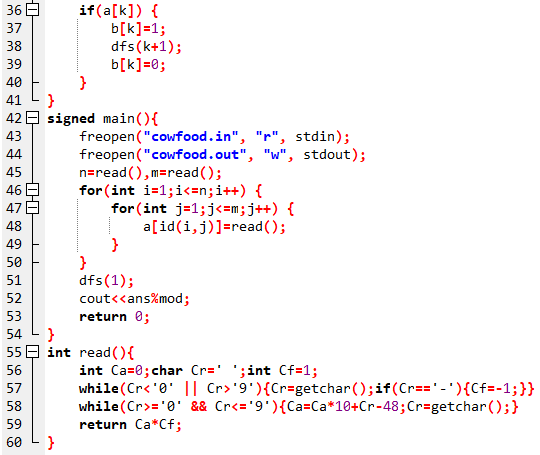
标程思路:
先考虑 1≤M≤12,1≤N≤12 的情况
设 f_{i,j} 表示第 i 行的方案是 j(是一个二进制数,用十进制来存储,第 k 位是 1/0(二进制)表示选或不选)时的方案数。
注意:下面的 j,k 都是一个合法的方案。
考虑转移:
假设当前已经进行到第 i 行,此时的方案是 j,上一行的方案是 k。
当 i=1 时,则它的所以合法方案都是正确的,所以 f_{1,j}=1
当 i\ne1 时,则合法方案的方案数是上一行的所有合法方案数,所以 f_{i,j}=f_{i,j}+f_{i-1,k}
设 F_{m} 表示宽为 m 的无障碍行的合法方案数。
则时间复杂度为 O(nF_{m}^2)。
再考虑 1≤M≤19,1≤N≤19 的情况
采用轮廓线 DP。设 f_{i,j,k} 表示当前点在 (i,j),轮廓线的状态是 k 的方案数
设 st_{i} 是一位二进制数,表示是否选择所在格子。
考虑转移:
对 x 的上面和左面是否是 1,分类讨论即可
时间复杂度 O(nm2^m)。
再进一步,考虑 1≤M≤21,1≤N≤120 的情况
在 1≤M≤12,1≤N≤12 时,我们用了缩小状态集合优化,使得时间复杂度从原本的 O(n4^m) 降到了 O(nF_{m}^2)。
所以为了让时间复杂度更小,我们也考虑让轮廓线 DP 也缩小状态集合。但似乎遇到一个瓶颈:在 1≤M≤12,1≤N≤12 时,它的状态是一整行,所以可以直接判断相邻确定合法;而轮廓线的状态可能分布在两行,就是说出现一组相邻都选的情况是合法的。难道不能确定合法吗?
因为它存在的相邻的地方就是行的分割处,所以把它记录下来,在 DP 时根据当前点的位置就单纯枚举“当前是分割点”的状态即可。
标程代码:
没打,就不放了
T3(23 -> 23)
题目描述
你的朋友们为了会见 IOI 回来的国家队选手准备了很多漂亮的
海报,现在就还差要考虑些细节了。
为了欢迎这些选手,你的 n 个朋友会拿着海报站成一个圈。为
了方便描述,我们把他们编号为朋友 1…n,其中对于 i ∈ [1,
n - 1],朋友 i 和朋友 i + 1 站在一起,且朋友 n 和朋友 1
站在一起。
每张海报都有一个美观度,其中朋友 i 拿着的海报的美观度为
a_i。当开始庆祝时,一些朋友会举起他们的海报。为了美观,不
能有 4 个或以上排在一起的朋友同时举起他们的海报。
为了能够丰富节目效果,你的朋友们还打算在庆祝过程中更换q
次海报。每次更换后,海报 pi 的美观度将变为 qi。你的朋友想
知道每次更换后在符合上述条件下的最大美观度之和。
你的任务是给出初始的美观度,求出初始以及各次更换后的最
大美观度之和。
输入
第一行一个整数 n,代表朋友总数。
接下来一行 n 个整数 ai,表示初始美观度。
第三行一个整数 q,代表海报更换次数。
接下来 q 行,每行两个整数 pi、vi,描述一次更换(将海报
pi的美观度变为 vi )。
输出
输出q+1行,依次表示初始时以及各次更换后,在 “不能有4个
或以上排在一起的朋友同时举海报” 条件下,最大美观度之和。
赛时思路:
对于每个询问,暴力枚举所有可能的情况,判断是否合法,取最大值即可
时间复杂度 O(q2^n)
赛时代码:


标程思路:
先考虑无修改:
设 dp_{i,j} 表示以 i 结尾,最后选了 j 个人的最大美观值。
考虑转移:
当 j=0 时, dp_{i,0}=\max\limits_{j=0,1,2,3}{dp_{i-1,j}}
当 j \in [1,3] 时, dp_{i,0}=dp_{i-1,j-1} + a_{i}
发现当 j=0 时,有带有 max 的方程,所以需要使用广义矩阵乘法 A \times B = C,其中 C_{i,j} = \max\limits_{k=1}{(A_{i,k} + B_{k,j})}
将转移方程写成矩阵的形式:
\left[ \begin{array}{cccc} dp_{i – 1,0}&dp_{i – 1,1}&dp_{i – 1,2}&dp_{i – 1,3} \end{array} \right] \\ \times \left[ \begin{array}{cccc} 0&a_i&-\infty&\infty \\ 0&-\infty&a_i&-\infty \\ 0&-\infty&-\infty&a_i \\ 0&-\infty&-\infty&-\infty \end{array} \right] \\ = \left[ \begin{array}{cccc} dp_{i,0}&dp_{i,1}&dp_{i,2}&d_i \end{array} \right]
又因为有结合律,所以:A \times B_{1} \times B_{2} \times \ldots \times B_{n} = A\times (\prod_{i=1}^{n}{B_{i}})
因为带修改,用线段树维护,每次修改都是一次线段树单点修改矩阵,每次询问直接用根节点即可。
因为是环,终点和起点也要满足不能连续超过 4 个人,比较无脑的方式是断环成链,不同起点要跑四遍线段树。
但因为是个环,所以 dp_{0,j}=dp_{n,j}
初始化:初始矩阵除了 dp_{0,j}=0 ,其他都是 −∞。
我们直接讨论以 n 结尾选了 j 个,此时答案矩阵只能选 dp_{n,j}。而对应在中间的转移矩阵,就是第 j 行,第 j 列的元素。所以在代码实现中,不需要维护初始矩阵和答案矩阵,最后只需统计线段树根节点矩阵对角线的最值即可。
标程代码:
没打,就不放了
T4(0 -> 100)
题目描述
著名的电子产品品牌SHOI刚刚发布了引领世界潮流的下一代电
子产品——概率充电器:
“采用全新纳米级加工技术,实现元件与导线能否通电完全由真
随机数决定!SHOI概率充电器,您生活不可或缺的必需品!能充
上电吗?现在就试试看吧!”
SHOI概率充电器由n-1条导线连通了n个充电元件。进行充电时,
每条导线是否可以导电以概率决定,每一个充电元件自身是否直
接进行充电也由概率决定。随后电能可以从直接充电的元件经过
通电的导线使得其他充电元件进行间接充电。
作为SHOI公司的忠实客户,你无法抑制自己购买SHOI产品的冲
动。在排了一个星期的长队之后终于入手了最新型号的SHOI概率
充电器。你迫不及待地将SHOI概率充电器插入电源——这时你突然
想知道,进入充电状态的元件个数的期望是多少呢?
输入
第一行一个整数:n。概率充电器的充电元件个数。充电元件由
1-n编号。
之后的n-1行每行三个整数a, b, p,描述了一根导线连接了编
号为a和b的充电元件,通电概率为p%。
第n+2行n个整数:qi。表示i号元件直接充电的概率为qi%。
输出
输出一行一个实数,为能进入充电状态的元件个数的期望,四
舍五入到小数点后6位小数。
赛时思路:
一眼树形 DP,但概率没学过,不会打。
赛时代码:
没学过概率,不会打。
标程思路:
首先我们看到这里每一个的贡献都是 1,所以我们要求的期望就是概率
就是 \sum_{i=1}^{n}{P_{i}}
其中 P_{i} 为节点 i 通电的概率
显然节点 i 通电有三种可能:
- 它自己来电了
- 它的子树里有一个点来电了传了过来
- 它的子树外面有一个点来电了传了过来
对于第一种情况,即为 P_{i}
对于第二种和第三种情况,可以使用树规里的 up and down 思想
设 h_{i} 表示第i个节点通电的概率,之后我们利用 up and down 思想:
在第一遍dfs的过程中,h_{i} 表示第 i 个节点通电的概率,且电一定来自它自己或者它的子树里(对应第一第二种情况),在第二遍dfs的时候被更新成为电来自于任何地方的概率(对应所有情况)
初始化:h_{i}=a_{i} \times 0.01
之后进行第一遍dfs,树形 dp 里的 up ,我们要将子树的信息合并给根,由于根通电还是有两种可能
- 根自己来电了
- 儿子来电,儿子通向根的边导电
显然这两种情况只需要满足一种就够了
我们考虑有两个事件 A,B,发生的概率分别是 P(A),P(B),那么至少发生一件的概率应该是 P(A)+P(B)-P(A) \times P(B)
所以我们合并根和子树的信息的时候,P(A)=h_{i},P(B)=h_{j}∗p_{i,j}
其中 i 是子树的根,j 是 i 的儿子,p_{i,j} 是这条边导电的概率
所以 h_{i}=P(A)+P(B)-P(A) \times P(B)
之后我们就要考虑 down 了,一个节点有点也有可能来自它的父亲,于是我们采用 down 的思想用父亲更新儿子
显然我们更新一位父亲的某个儿子,显然我们只能用其他点来电传到父亲的概率来更新这个儿子
于是我们设 P(B)=h_{j}∗p_{i,j}
而且有 P(A)+P(B)−P(A)∗P(B)=h[i]
我们要求的是 P(A) 即除了 j 这棵子树其他点来电使得 i 有电的概率
于是解一下这个方程 P(A)−P(A)∗P(B)=h_{i}−P(B) P(A)∗(1−P(B))=h_{i}−P(B) P(A)=\frac{h_{i}-P(B)}{1-P(B)}
之后就没有啦,同时还有一个非常坑的地方就是如果 P(B)=h_{j}∗p_{i,j}=1
那么除以 1−P(B) 肯定会出错,由于 h_{i} 都已经是 1 了,显然没有什么必要去更新它了,于是可以直接跳过这一层接着往下更新就好了
标程代码:

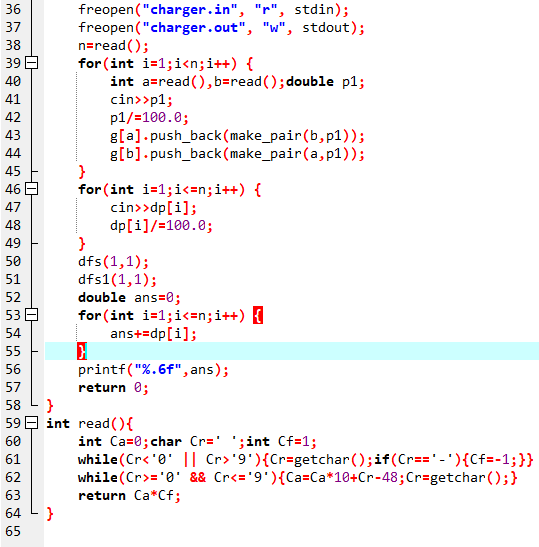
下午
改题目
晚上
打博客
博客从4:00打到了5:00,又从7:00打到了9:30