今天算是我第一天来到中山纪念中学集训，前两天在家里休息并参加了这里的模拟比赛，一次六十几分，一次一百一十分，都是无脑暴力骗分，没有技术含量，毕竟刚从海亮回来，脑子得换一下（被数学物理折磨惨了）

今天下午听课，讲整体二分，完全听不懂啊。Oh,god!That’s too bad.
晚自习的时候打了一下他们早上讲的题

斯坦纳树

令人惊奇，这玩意最开始竟然是个几何问题，后来才推广成图论上的问题

对于给定的无向图G,再给出一个点集S（S为V的子集），现要找出一个连通图G1(G1是G的子图)使的V1包含S，并且对于边集E1来说，其边权总和最小（每条边的边权总是大于0）

这样的G1事实上就是斯坦纳树。为什么G1会是一个树状结构？原因也很简单，若G1中包含了环的话，将环中一条边删去并不破坏原图的连通性，显然会比原图更优

那么怎么找出这个树呢？
我们需要状压dp

dp[i][j]表示选取点i作为根节点时，j选点状态下的最小边权和
对于点集S来说，考虑比较其与其子集和子集的补集的dp之和
有状态转移方程dp[i][S]=min(dp[i][S],dp[i][T]+dp[i][S^T])（T是S的子集）

并且，我们考虑使用最短路径的算法来更新dp的值，因为我们可将树看作是多条链组成的
对于一条链的路径，我们也有dp[nxt][S]=min(dp[nxt][S],dp[now][S]+w)
这里我们可以选择spfa或dijkstra算法

于是综上有以下代码

#include
using namespace std;
#define long long int
const int N=510,K=11;
int n,m,k,p[N];
int dp[N][1<<K];
struct edge{
    int to,nxt,w;
}e[N<dp[now][s]+e[i].w){
                dp[nxt][s]=dp[now][s]+e[i].w;
                if(!vis[nxt]){
                    q.push(nxt);
                    vis[nxt]=1;
                }
            }
        }
    }
}
int main(){
    memset(dp,0x7f,sizeof(dp));
    cin>>n>>m>>k;
    for(int i=1;i>u>>v>>w;
        add(u,v,w);add(v,u,w);
    }
    for(int i=1;i>p[i];
        dp[p[i]][1<<(i-1)]=0;
    }
    for(int s=0;s<(1<<k);s++){
        for(int i=1;i<=n;i++){
            for(int t=s&(s-1);t;t=(t-1)&s){
                dp[i][s]=min(dp[i][s],dp[i][t]+dp[i][s^t]);
            }
            if(dp[i][s]<1e9)q.push(i);
        }
        spfa(s);
    }
    cout<<dp[p[1]][(1<<k)-1]; 
    return 0;
}

luogu P4784

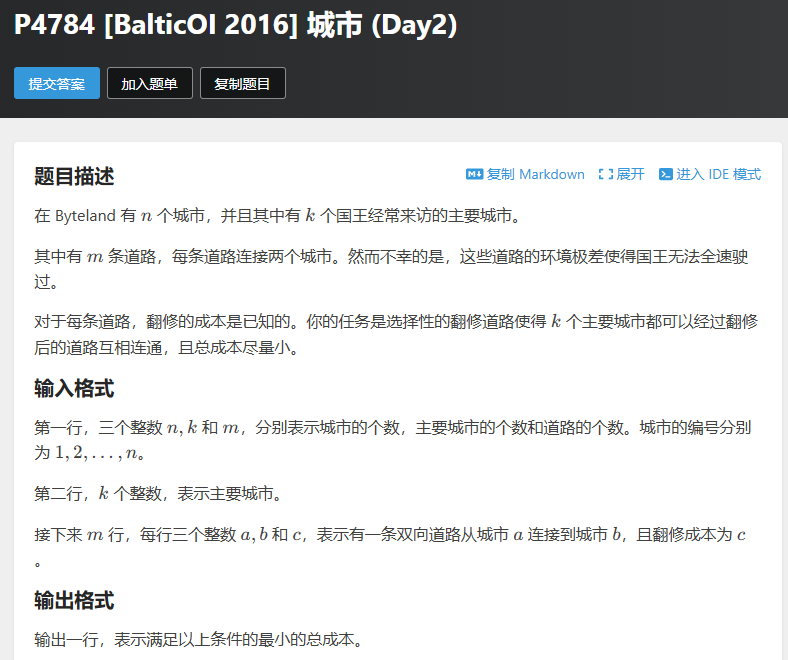
这题测试数据有卡spfa，所以上面的模板spfa要换成dijkstra

#include
using namespace std;
const int N=1e5+100,K=5;
typedef long long L;
const L MAXN=2e15;
int n,m,k;
int p[N];
L dp[N][1<<K];
int head[N],cnt;
vector<pair >G[N];
int vis[N];
priority_queue<pair,vector<pair >,greater<pair > >q;
void dijkstra(int s){
    memset(vis,0,sizeof(vis));
    while(!q.empty()){
        int now=q.top().second;q.pop();
        if(vis[now])continue;
        vis[now]=1;
        for(int i=0;idp[now][s]+w){
                dp[nxt][s]=dp[now][s]+w;
                q.push({dp[nxt][s],nxt});
            } 
        }
    }
}
int main(){
    memset(dp,0x3f,sizeof(dp));
    cin>>n>>k>>m;
    for(int i=1;i>p[i];
        dp[p[i]][1<<(i-1)]=0;
    }
    for(int i=1;i>u>>v>>w;
        G[u].push_back({w,v});
        G[v].push_back({w,u});
    }
    for(int s=0;s<(1<<k);s++){
        for(int i=1;i<=n;i++){
            for(int t=s&(s-1);t;t=(t-1)&s){
                dp[i][s]=min(dp[i][s],dp[i][t]+dp[i][s^t]);
            }
            if(dp[i][s]<MAXN)q.push({dp[i][s],i});
        }
        dijkstra(s);
    }
    cout<<dp[p[1]][(1<<k)-1];
    return 0;
}