早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
讲算法和学算法
1. 最小斯坦纳树
定义:
斯坦纳树问题是组合优化问题,与最小生成树相似,是最短网络的一种。最小生成树是在给定的点集和边中寻求最短网络使所有点连通。而最小斯坦纳树允许在给定点外增加额外的点,使生成的最短网络开销最小。
背景:
19世纪初叶,柏林大学几何方面的著名学者斯坦纳,研究了一个非常简单却很有启示性的问题:将三个村庄用总长为极小的道路连接起来。从数学上说,就是在平面内给定三个点 A、B、C 找出平面内第四个点 P,使得和数 a+b+c 为最短,这里 a、b、c 分别表示从 P 到 A、B、C 的距离。
问题的答案是:
- 如果三角形 ABC 的每个内角都小于 120° ,那么 P 就是使边 AB、BC、AC 对该点所张的角都是 120° 的点。
- 如果三角形 ABC 的有一个角,例如 C 角,大于或等于 120° ,那么点 P 与顶点 C 重合。
推广:
- 在斯坦纳问题中,给定了三个固定点 A,B,C 。很自然地可以把这个问题推广到给定 n 个点 A_1,A_2,\cdots,A_n 的情形;我们要求出平面内的点 P ,使距离和 a_1+a_2+\cdots+a_n 为极小,其中 a_i 是 P 到 A_i 的距离。
- 考虑到点的其他相关因素,加入了权重的表示。 n 个点的其他相关因素可以换算成一个权重表示,求出平面内的点 P ,使距离与权重的乘积的总和 a_1\cdot w_1+a_2\cdot w_2+\dots+a_n\cdot w_n 为极小,其中 w_i 是每个点的权重。
- 数学上表述成:给定 n 个点 A_1,A_2,\cdots,A_n ,试求连接此 n 个点,总长最短的直线段连接系统,并且任意两点都可由系统中的直线段组成的折线连接起来。他们将此新问题称为 斯坦纳树问题。在给定 n 个点的情形,最多将有 n-2 个复接点(斯坦纳点)。过每一斯坦纳点,至多有三条边通过。若为三条边,则它们两两交成 120^{\circ} 角;若为两条边,则此斯坦纳点必为某一已给定的点,且此两条边交成的角必大于或等于 120^{\circ} 。
转化:
我们将斯坦纳树的问题模型以图论形式呈现。
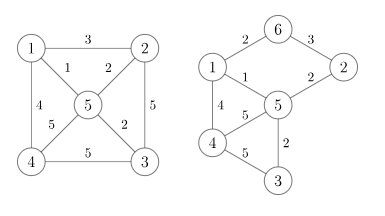
对于形式一,如果令关键点为 {1,2,3,4} ,可以发现若直接将这四个关键点相连的最小边权和是 12 ,显然这不是最优的。如果考虑使用 5 号节点那么最小边权和就会是 9 ,得到一个更优的答案。
对于形式二,如果令关键点为 {1,2,3,4} ,可以发现这四个关键点中的一些点甚至没有直接相连的边,必须考虑使用复接点(斯坦纳点)。这时将 5 号考虑进去可以得到最小边权和 9 。
并且我们可以发现在两张图中 1 号和 4 号的斯坦纳点是退化的,被 1 号或 4 号代替了。
例题:
1. 【模板】最小斯坦纳树
- 题意:给定连通图 G 中的 n 个点与 k 个关键点,连接 k 个关键点,使得生成树的所有边的权值和最小。
- 思路:使用状态压缩动态规划来求解。用 f(i,S) 表示以 i 为根的一棵树,包含集合 S 中所有点的最小边权值和。
- 考虑状态转移:
(I) 首先对连通的子集进行转移,f(i,S)\leftarrow \min(f(i,S),f(i,T)+f(i,S-T))
(II) 在当前的子集连通状态下进行边的松弛操作,f(i,S)\leftarrow \min(f(i,S),f(j,S)+w(j,i)) - 代码:


2. [BalticOI 2016] 城市 (Day2)
- 题意:选择翻修道路使得 k 个主要城市都可以经过翻修后的道路互相连通,且总成本尽量小。
- 思路:使用状态压缩动态规划来求解。用 f(i,S) 表示以 i 为根的一棵树,包含集合 S 中所有点的最小边权值和。
- 考虑状态转移:
(I) 首先对连通的子集进行转移,f(i,S)\leftarrow \min(f(i,S),f(i,T)+f(i,S-T))
(II) 在当前的子集连通状态下进行边的松弛操作,f(i,S)\leftarrow \min(f(i,S),f(j,S)+w(j,i)) - 代码:


3. [WC2008] 游览计划
- 题意:一个 n\times m 的图 A 。
(I) 如果 A_{i,j}=0 ,则表示 {i,j} 为给定的点。
(II) 如果 A_{i,j} \ne 0 ,则表示 {i,j} 的点权。
求给定的点联通的最小代价。 - 思路:这道题是求点权和最小的斯坦纳树。使用状态压缩动态规划来求解。用 f(i,S) 表示以 i 为根的一棵树,包含集合 S 中所有点的最小点权值和。 a_i 表示点权。
- 考虑状态转移:
(I) 首先对连通的子集进行转移,f(i,S)\leftarrow \min(f(i,S),f(i,T)+f(i,S-T)-a_i) 由于此处合并时同一个点 a_i ,会被加两次,所以减去。
(II) 在当前的子集连通状态下进行边的松弛操作,f(i,S)\leftarrow \min(f(i,S),f(j,S)+w(j,i)) - 代码:



2. 状压 DP
定义:
状压 DP 是动态规划的一种,通过将状态压缩为整数来达到优化转移的目的。
例题:
1. [SCOI2005] 互不侵犯
- 题意:在 N\times N 的棋盘里面放 K 个国王 (1 \leq N \leq 9, 1 \leq K \leq N \times N) ,使他们互不攻击,共有多少种摆放方案。国王能攻击到它上下左右,以及左上左下右上右下八个方向上附近的各一个格子,共 8 个格子。
- 思路:设 f(i,j,l) 表示前 i 行,第 i 行的状态为 j ,且棋盘上已经放置 l 个国王时的合法方案数。对于编号为 j 的状态,我们用二进制整数 sit(j) 表示国王的放置情况, sit(j) 的某个二进制位为 0 表示对应位置不放国王,为 1 表示在对应位置上放置国王;用 sta(j) 表示该状态的国王个数,即二进制数 sit(j) 中 1 的个数。例如,如下图所示的状态可用二进制数 100101 来表示(棋盘左边对应二进制低位),则有 sit(j)=100101_{(2)}=37 , sta(j)=3 。

- 考虑状态转移:设上一行的状态编号为 x ,在保证当前行和上一行不冲的前提下,枚举所有可能的 x 进行转移,转移方程: f(i,j,l)=\sum f(i-1,x,l-sta(j))
- 代码:


2. [POI 2004] PRZ
- 题意:有 n 个人需要过桥,第 i 的人的重量为 w_i,过桥用时为 t_i 。这些人过桥时会分成若干组,只有在某一组的所有人全部过桥后,其余的组才能过桥。桥最大承重为 W,问这些人全部过桥的最短时间。(100\le W \le 400,1\le n\le 16,1\le t_i\le 50,10\le w_i\le 100)
- 思路:我们用 S 表示所有人构成集合的一个子集,设 t(S) 表示 S 中人的最长过桥时间, w(S) 表示 S 中所有人的总重量,f(S) 表示 S 中所有人全部过桥的最短时间。
- 考虑状态转移:\begin{cases} f(\varnothing) = 0 \\ f(S) = \min\limits_{\substack{T \subseteq S; w(T) \leq W}} {t(T) + f(S \setminus T) }\end{cases}
- 代码:

3. 树形 DP
定义:
树形 DP ,即在树上进行的 DP 。由于树固有的递归性质,树形 DP 一般都是递归进行的。
例题:
1. 没有上司的舞会
- 题意:某大学有 n 个职员,编号为 1 \sim N 。他们之间有从属关系,也就是说他们的关系就像一棵以校长为根的树,父结点就是子结点的直接上司。现在有个周年庆宴会,宴会每邀请来一个职员都会增加一定的快乐指数 a_i ,但是呢,如果某个职员的直接上司来参加舞会了,那么这个职员就无论如何也不肯来参加舞会了。所以,请你编程计算,邀请哪些职员可以使快乐指数最大,求最大的快乐指数。
- 思路:设 f(i,0/1) 代表以 i 为根的子树的最优解(第二维的值为 0 代表 i 不参加舞会的情况, 1 代表 i 参加舞会的情况)。
- 考虑状态转移:
(I) 上司不参加舞会时,下属可以参加,也可以不参加,此时有 f(i,0) = \sum\max {f(x,1),f(x,0)}
(II) 上司参加舞会时,下属都不会参加,此时有 f(i,1) = \sum{f(x,0)} + a_i - 代码:

4. 最小生成树(Prim 算法)
定义:
我们定义无向连通图的 最小生成树(Minimum Spanning Tree,MST)为边权和最小的生成树。
注意:只有连通图才有生成树,而对于非连通图,只存在生成森林。
例题:
1. 【模板】最小生成树
- 题意:给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。
- 思路:我们可以把最终的最小生成树视为一个集合(下文称 mst 点集),一开始它只有结点 1 ,后面每次遍历加入新的点,最终形成我们要的最小生成树。我们定义 dis_i 为与 mst 点集直接相连的结点 i 到 mst 点集的距离,如果结点 i 与 mst 点集并不直接相连,则 dis_i=+∞ 。由于 1 号结点一开始就在集合里,应初始化 dis_1=0 。每次遍历寻找 dis 最小的点加入,然后更新与这个点相邻的点的 dis 。对于判连通,如果某一次在找新点时发现找不到,那么图是不连通的。
- 代码:

下午
打题目
晚上
打博客
博客从7:00打到了9:30