模拟赛
T1
传送门
某集训T1升级版
先不考虑环的情况,定义f_i表示以第i位结尾的符合题意子序列最长长度,则有
f_i=\max\limits_{j=1}^{i-1}f_j+1(|a_j-a_i|\ne 1)
暴力转移时间复杂度O(n^2)。
但实际上不满足|a_j-a_i|\ne 1的不同a_j很少,只有a_i-1和a_i+1,所以可以只维护最大的3个f_j使3个对应的a_j互不相等,这样对于任意的i其中一定有至少一个j满足转移条件,时间复杂度O(n)。
如果考虑环,即首尾数字差不为一,类似的,可以只维护少量的状态进行转移,只枚举前9个不同的数作为开头(题解说只要枚举5个),时间复杂度O(n)。
T2
传送门
又是非常神奇的一道题。(数据也很神奇,赛时O(n^2)能80pts)
二分答案,对于每个二分值mid,将大于mid的a_i记为1,否则记为0。
由于01序列的特殊性质可以使用线段树对局部区间在O(logn)的时间进行神奇的排序操作,然后根据修改后的a_q调整二分区间。
T3
传送门
处理出原图的最短路径树,如果翻转树上的边暴力dij,否则直接利用最短路径树O(1)查询,时间复杂度O(n^3+m)。
T4
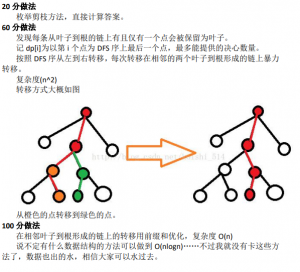
传送门
题解如图: