早上7:30,我们来到了这与我们泉州第一中学有长达2个汉字的最长公共子序列的中山纪念中学。
上午
打比赛—-2025.07.27【提高B组】模拟赛
传送门
T1(30 -> 100)
题目描述
被认为天才的小头遇到麻烦了!!这天数学课老师给出了一
道难题,而小头居然没能在3秒内解决,可见此题难度之大。
问题是这样的:n个整数围成一个环,老师要求选出其中的
若干数,使得选中的数所组成的环中,两个相邻数的差的绝对
值不等于1。在满足这个前提下,问最多能取多少个数。
输入
第一行一个正整数n,表示有n个数
第二行n个整数,a1、a2……an 按顺时针方向围成一个环。
输出
一个正整数,即表示最多能选多少个数。
赛时思路:
1.暴力枚举出所有可能的环
2.然后判断是否合法,求长度的最大值
赛时代码:

标程思路:
法一:
1.设dp[i]表示取第i个数时的最多选的个数
2.状态转移方程:dp[i]=dp[j]+1(1≤j≤i-1 && abs(a[j]-a[i])!=1)
3.用线段树来维护数值为a[i]时dp[i]的最大值
法二:
1.设dp[i]为距离起始点为i-1的点的贡献
2.每次记录三个最大值用于维护,然后枚举一个向后的点去转移,因为每个点作为起点或者是加入别的起点的答案,那么只需要枚举一定量不同的起点即可(据推出大概是 10)
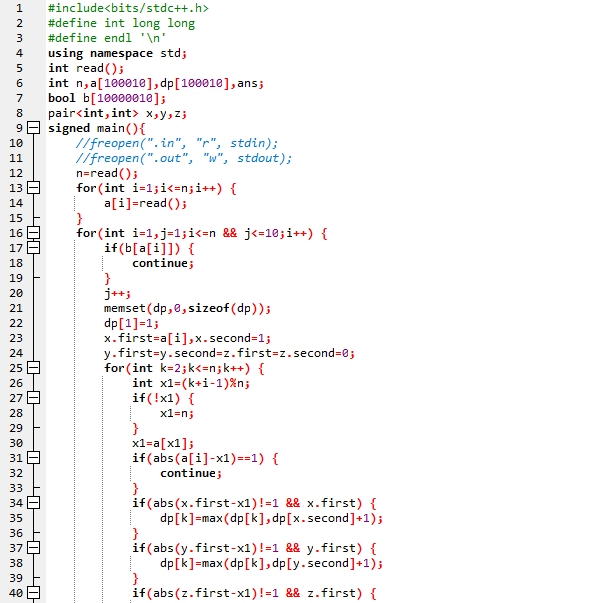
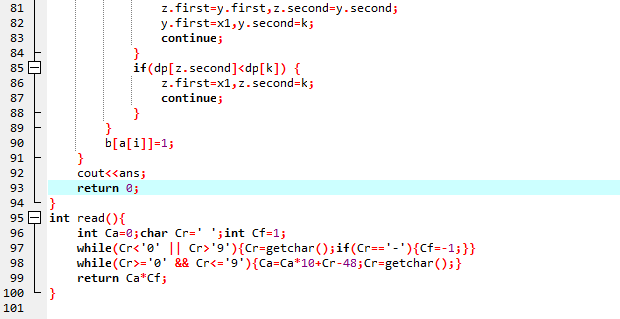
标程代码:

T2(60(80) -> 80)
题目描述
在2016年,佳媛姐姐喜欢上了数字序列。因而他经常研究关
于序列的一些奇奇怪怪的问题,现在他在研究一个难题,需要你
来帮助他。
这个难题是这样子的:给出一个1到n的全排列,现在对这个
全排列序列进行m次局部排序,排序分为两种:
(0,l,r) 表示将区间 [l,r] 的数字升序排序
(1,l,r) 表示将区间 [l,r] 的数字降序排序
最后询问第q位置上的数字。
输入
输入数据的第一行为两个整数n和m。n表示序列的长度,m表
示局部排序的次数。1≤n,m≤10⁵
第二行为n个整数,表示1到n的一个全排列。
接下来输入m行,每一行有三个整数op,l,rop为0
代表升序排序,op为1代表降序排序,l,r表示排序的区间。
最后输入一个整数q,q表示排序完之后询问的位置,1≤q≤n。
输出
输出数据仅有一行,一个整数,表示按照顺序将全部的部分
排序结束后第q位置上的数字。
赛时思路:
暴力,可以得80分
赛时代码:

标程思路:
1.对于30分,直接按照操作暴力即可。
2.对于100分显然是不能直接暴力的。可以想到二分答案。分析时间复杂度,发现对于每次操作,必须不大于log2(n)才能,线段树!对于二分的答案,将大于这个的数变为1,小于的变为0。对于一个区间,从小到大排序就是把0堆在前面,1放在后面,从大到小排序则相反。这可以用线段树区间修改来做到。最后再按照第k位看看是0还是1来修改区间。
标程代码:
没打,就不放了
T3(0(5) -> 100)
题目描述
JOI王国共有N个城市,这些城市从1到N编号。共有M条公交线
路连接这些城市,这些线路从1到M编号。第i(1≤i≤M)条公交线是
从城市U_i到城市V_i的,票价为C_i日元。如果乘客乘坐第i条公
交线,他只能在城市U_i上车,在城市V_i下车。从一个城市到另
一个城市可能有多条公交线。
不久,JOI王国将举办奥运会。K理事长是JOI王国交通部部
长。他会在奥运会之前选择最多一条公交线,并翻转这条公交线
的起点和终点,但不改变票价。换句话说,如果他选择第i条公交
线,在奥运会期间它将不会从U_i城市开往V_i城市,而是从V_i城
市开往U_i城市,但票价仍为C_i日元。翻转一条公交线需要D_i
日元,并且这个钱是K理事长出的。为了避免迷惑行为,在奥运会
期间不允许翻转公交线。
因为K理事长是JOI王国的交通部部长,在奥运会期间他会使
用这些公交线在城市1和城市N之间往返。通过恰当地选择翻转某
条(或不翻转任何)公交线,他想要最小化往返城市1和城市N的
公交总票价与翻转公交线的代价和。
现给定城市数和公交线情况,写一个程序求出这个最小代价
和。如果不能通过翻转某条公交线来达到往返城市1与城市N的目
的,请输出-1。
输入
第一行两个整数N,M,意义如题目描述;
接下来M行,每行四个整数U_i,V_i,C_i,D_i,意义如题目
描述。
输出
输出一行一个整数,如果可以通过翻转某条(或不翻转任何)
公交线使得可以往返于城市1与城市N,输出往返所需公交总票价
与翻转公交线的代价和的最小值,否则输出-1。
赛时思路:
Dijkstra+暴力
赛时代码:
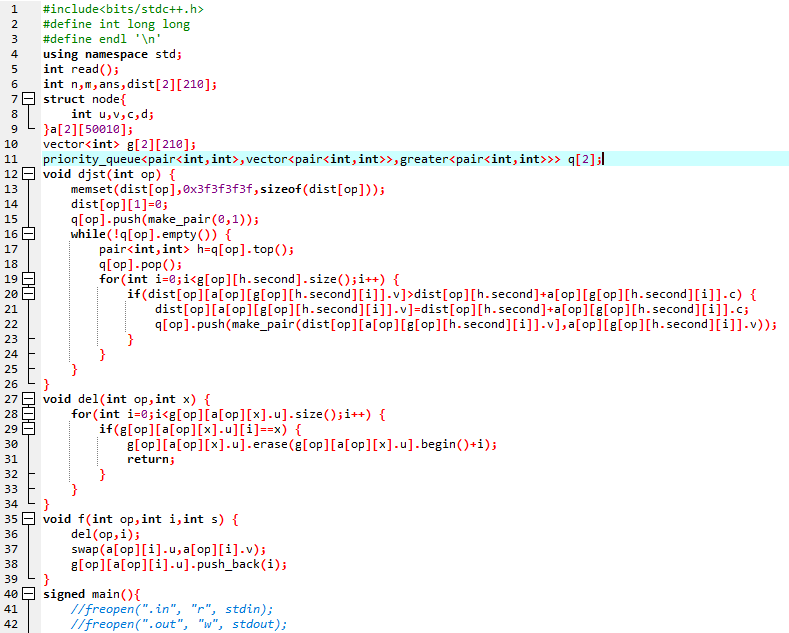

标程思路:
1.对于5分,暴力枚举更改边,然后直接上dijkstra。
2.对于100分,考虑对刚刚的暴力进行优化,发现对复杂度影响最大的其实是m
在每次枚举边,修改边,重新计算的过程中可以先求出最短路径生成树
对于一条边:
(1)不在最短路径生成树中:就是原最短路,必须经过该边,但路径上的其他边都必须是在最短路径树上
(2)在最短路径生成树中:翻转后,重新计算即可
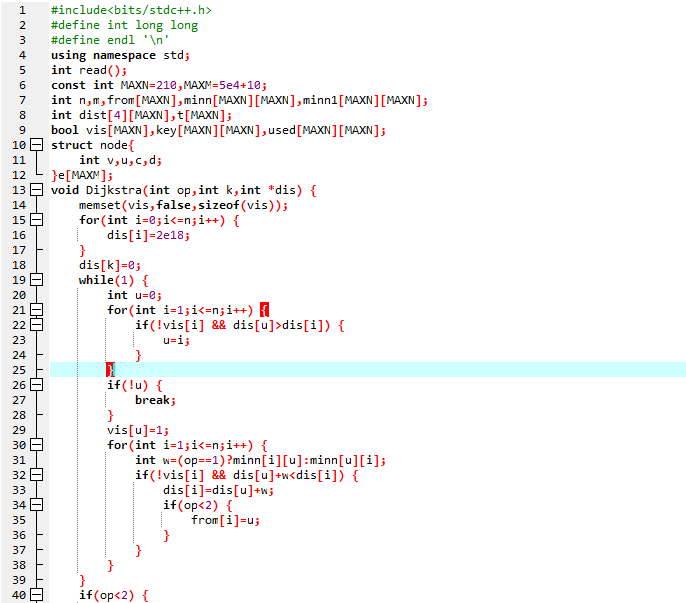
标程代码:


T4(0 -> 0)
题目描述
Temmie村里有很多提米树,上面长满了Temmie薄片。一天,
Flowey来到Temmie村做客,Temmie们想要送给它一棵提米树。
对于这棵提米树,满足这样的性质:
1. 这棵树可以看做一棵n个点的无向无环图,每个点上长了
一定数量的Temmie薄片,薄片数量记为这个点的权值,这些点被
标记为1到n的整数,其中1号点是树的根,没有孩子的点是树上
的叶子。
2. 对于这棵树进行深度优先搜索,每个点从左到右按顺序
遍历每个孩子,得到这棵树的DFS序。
3. 定义(a,b)是一对相邻的叶子,当且仅当没有其它的叶子
节点在DFS序上在a,b之间。每对相邻的叶子都会产生一个代价,
代价为a到b路径上(不包含 a,b)的点中,最大点权值。
4. 提米树可以提供决心,一棵提米树能提供的决心的数量
是树上所有叶子上长的Temmie薄片数量和,减去所有相邻叶子的
代价.
Flowey虽然不是以Temmie薄片为食的生物,但是它需要决
心。这棵提米树能提供的决心太少了,Temmie们决定对这棵树进
行若干次剪枝(可以不剪枝),使得这棵树能提供的决心最多。
一次剪枝定义为:如果一个点的孩子都是叶子,就可以把它
所有的孩子剪掉。
输入
输入数据的第一行为一个正整数n,代表提米树上点的数量。
接下来n行,对于每行:
第一个数为一个正整数,代表这个点上Temmie薄片的数量
第二个数为一个整数num,代表这个点孩子的数量
接下来num个数,依次表示这个点从左到右的孩子。
输出
输出包含一个数,为这棵树剪枝后最多能提供的决心的数量
赛时思路:
dfs+倍增求lca+暴力
赛时代码:




标程思路: