上午练习赛:
T1
题目描述
n个整数围成一个环,老师要求选出其中的若干数,使得选中的
数所组成的环中,两个相邻数的差的绝对值不等于1。在满足这个前
提下,问最多能取多少个数。
输入
第一行一个正整数n,表示有n个数
第二行n个整数,a1、a2……an 按顺时针方向围成一个环。
输出
一个正整数,即表示最多能选多少个数。
样例输入
5
1 2 3 5 2
样例输出
3
提示
【样例解释】
最多能选3个数
既选择(1,3,5)或者(2,5,2)
【数据范围】
30% : n ≤ 10
50% : n ≤ 100
70% : n ≤ 1000
100% :n ≤ 100000,ai ≤ 1100000
30% : 搜索
50% : 即枚举起点将环化成一行,然后暴力DP \Rightarrow O(N^3)(该算法优化后可以得60~70分)
100%法一 : 用dp[i]表示以第i个数结尾最多能选多少个数。发现枚举完起点把环转化成一行后,那么在求dp[i]时只需要记录dp[1]到dp[i-1]里前3大的数就可以了(显然3个不同数中至少有一个和a[i]的绝对值不等于1)。同理,在枚举起点时也只要枚举前9个不同的数 \Rightarrow O(N)
100%法二 : 也有用DP + 线段树的,也能过 \Rightarrow O(nlogn)
DP具体方法:
初始化 :dp[i] = 1
遍历 : for \quad i \quad 1 \Rightarrow n
\qquad for \quad j \quad 1 \Rightarrow i – 1
转移条件 : if(|a[i] – a[j]| \ne 1)
转移方程 : dp[i] = max(dp[i], dp[j] + 1)
最后用线段树维护
T2
题目描述:
给定一个由1,2....n组成的长度为n的序列(每个数都不相同),
要求对这个序列进行m次局部排序,排序分为两种:
{0, l, r} 表示将区间[l,r]中的数字升序排序
{1, l, r} 表示将区间[l,r]中的数字降序排序
最后询问第q个位置的数字
输入:
第一行两个整数n和m,n表示序列长度,m表示局部排序的次数
第二行n个整数,表示一个长度为n的序列
接下来m行,每行三个整数op,l和r,op为0表示升序排序,op
为1表示降序排序,l和r表示排序的区间范围
最后一个整数q,q表示要询问的位置
输出:
仅一行,一个整数,表示全部排序后第q个位置的数
样例输入
6 3
1 6 2 5 3 4
0 1 4
1 3 6
0 2 4
3
样例输出
5
数据范围限制
30% : 1 <= n <= 100, 1 <= m <= 100
100% : 1 <= n <= 10^5, 1 <= m <= 10^5, 1 <= q <= n
30% :模拟题目要求暴力求解 \Rightarrow O(nmlogn)
100% :二分答案,每次二分的值为a,将整个序列中大于等于a的值变为1,小于a的值变成0。这样序列中只有0和1,对于每一次部分排序,通过线段树的区间更新,若为升序排序,则把该区间的0全部排在区间前段,1排在区间后段,最后全部部分排序结束后,检验位置p上的值是1还是0,来继续调整下一次二分,直到二分结束 \Rightarrow O(mlog^2n)
(实际本题暴力直接sort有80分)
T3
部分分 : 暴力枚举翻转每条边,每个进行一遍 dijkstra \Rightarrow O(n^2m)
100% : 详见洛谷P6880题解
T4


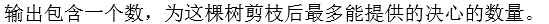
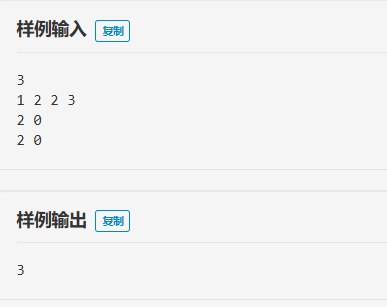

题解: