被一堆新高一和新初三的包围了!
我要退役![大哭]
TG – A
[T1]
(53 -> 100)
原题题意:
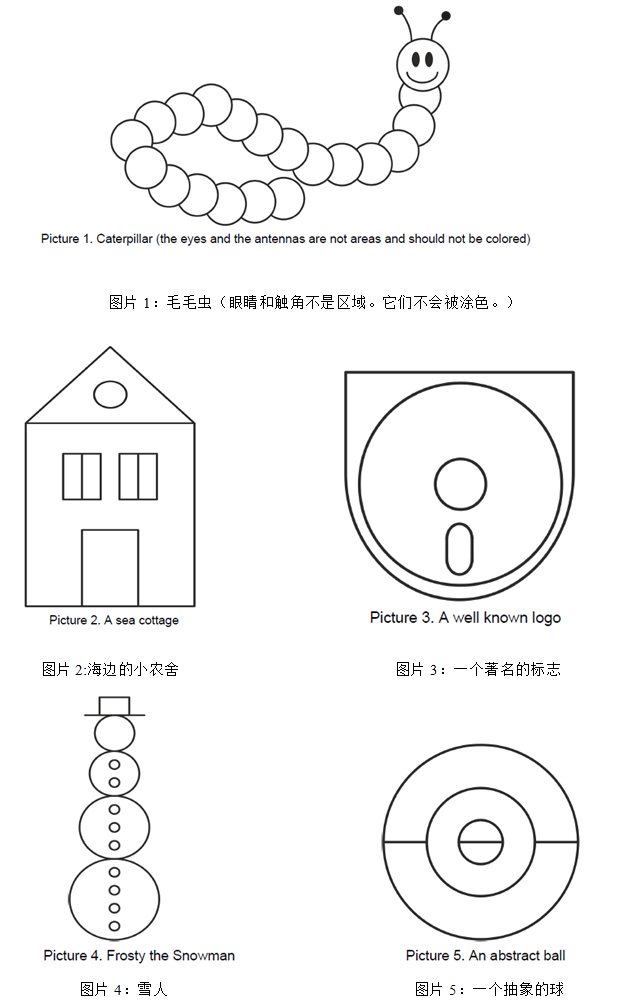
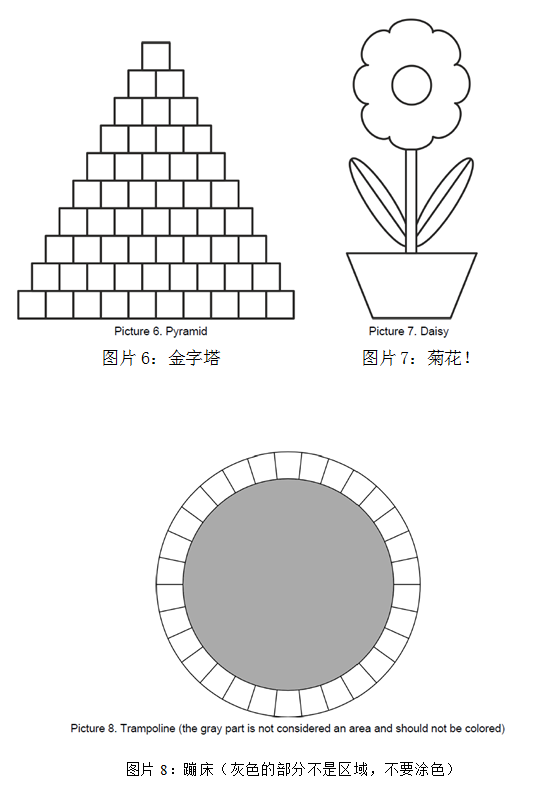
给你 8 个图,最多用三种颜色染, 还要保证相邻区域(共边/共点)不会染成相同颜色。
现在有 k 种颜料,问对于特定的图有多少种染色方法。
注意不考虑轴对称情况,对于两种染色方案,只要有一个位置不一样,就是不同的染色方法。
好吧这个 TJ 还是太考验注意力了。
对于 2,5,6,7 这四种,是较好处理的,因为都要使用三种颜色。
对于 1,3,4,8 这四种,注意计算用三种颜料填涂方案数时减去用仅用两种颜料填涂的方案数。
然后我忘了减了。
然后就挂了。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int main()
{
freopen("color.in", "r", stdin);
freopen("color.out", "w", stdout);
int op, k;
scanf("%d%d", &op, &k);
LL C2 = k * (k - 1) / 2, C3 = k * (k - 1) * (k - 2) / 6LL, res;
if (op == 1)res = C2 * 2LL + C3 * (3LL * ((1LL << 19) - 2LL));
else if (op == 2)res = C3 * 3LL * 2LL * 2LL * 2LL * 2LL * 2LL;
else if (op == 3)res = C2 * 2LL + C3 * 3LL * (2LL * 2LL * 2LL - 2LL);
else if (op == 4)res = C2 * 2LL + C3 * 3LL * (2LL * (2LL * 2LL * 2LL) * (2LL * 2LL * 2LL * 2LL) * (2LL * 2LL * 2LL * 2LL * 2LL) - 2);
else if (op == 5)res = C3 * 3LL * 2LL * 2LL;
else if (op == 6)res = C3 * 3LL * 2LL;
else if (op == 7)res = C3 * 3LL * 2LL * 2LL * 2LL * 2LL * 2LL;
else if (op == 8)res = C2 * 2LL + C3 * ((1LL << 30LL) - 4);
printf("%lld", res);
return 0;
}
[T2]
(40 -> 100)
TJ里有原,凑合着用
不行了一看到 DP 立马弃疗。
但是似乎做法还很多的。
预处理组合数与阶乘
定义 f_{i, j} 表示 对于前 i 个班级,存在 j 组连续的情况的方案数。(将同一班级的看为一人)
答案为 $f{n, 0} * \prod{i = 1}^{n} \prod {j = 1} ^ {r_i} j$
转移非常不明显(?)
$$f_{i, j + w_i – k – t} = f_{i, j + w_i – k – t} + f_{i – 1, j} \cdot \binom{j}{t} \cdot \binom{w_i – 1, k – 1} \cdot \binom{sum_{i – 1} + 1 – j}{k – t}$$
$k$ 为第 $i$ 个班分为 $k$ 组(每一组连续)
$t$ 为 $k$ 组中有 $t$ 组插在之前的 $j$ 个位置上
$\binom{j}{t}$ 是在j个位置中枚举t个位置
$\binom{w_i – 1, k – 1}$是将第 $i$ 个班的人分为 $k$ 组的方案数
$\binom{sum_{i – 1} + 1 – j}{k – t}$是在剩下的位置中枚举位置。
当然还可以用二项式反演,但是忘完了。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 55, M = 1505, mod = 1e9 + 7;
int n, w[N], sum[N];
LL C[M][M], fac[M], f[N][M];
int main()
{
freopen("photo.in", "r", stdin);
freopen("photo.out", "w", stdout);
fac[0] = C[0][0] = 1;
for (int i = 1; i < M; i ++)
{
fac[i] = fac[i - 1] * i % mod;
for (int j = 0; j < M; j ++)
{
if (!j)C[i][j] = 1;
else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mod;
}
}
scanf("%d", &n);
for (int i = 1; i <= n; i ++)
{
scanf("%d", &w[i]);
sum[i] = sum[i - 1] + w[i];
}
f[1][sum[1] - 1] = 1;
for (int i = 2; i <= n; i ++)
{
for (int j = 0; j <= sum[i - 1]; j ++)
{
if (!f[i - 1][j])continue;
for (int k = 1; k <= w[i]; k ++)
{
for (int t = 0; t <= min(k, j); t ++)f[i][j + w[i] - k - t] = (f[i][j + w[i] - k - t] + (f[i - 1][j] * C[j][t] % mod * C[w[i] - 1][k - 1] % mod * C[sum[i - 1] + 1 - j][k - t] % mod) % mod) % mod;
}
}
}
LL res = f[n][0];
for (int i = 1; i <= n; i ++)res = res * fac[w[i]] % mod;
printf("%lld", res);
return 0;
}
[T3]
(30 -> 100)
TJ有原,凑合着用
没想到是折半搜索。
想到了基本上就没了,记三个状态, i 表示当前点, S 表示遍历情况, dist 表示当前所走过距离。
注意这个 hash_table 需要自己写, unordered_map 在 GDNOJ 上实现的效率实在是太差了。
#include <bits/stdc++.h>
using namespace std;
const int N = 15;
int n, m, res;
int w[N][N], bit[N];
typedef long long LL;
unordered_map<LL, int> mp;
const int Size = 2e7 + 5, mod = 1e7 + 19;
struct node
{
int u, S, dist, cnt;
}table[Size];
void Hash(int u, int S, int dist)
{
int cur = 1LL * u * S % mod * dist % mod;
while(table[cur].cnt)
{
if (table[cur].u == u && table[cur].S == S && table[cur].dist == dist)
{
table[cur].cnt ++;
return;
}
cur ++;
if (cur >= Size) cur = 0;
}
table[cur] = {u, S, dist, 1};
}
int get_hash(int u, int S, int dist)
{
int cur = 1LL * u * S % mod * dist % mod;
while(table[cur].cnt)
{
if (table[cur].u == u && table[cur].S == S && table[cur].dist == dist)return table[cur].cnt;
cur ++;
if (cur >= Size) cur = 0;
}
return 0;
}
void dfs1(int step, int u, int S, LL dist)
{
if (dist > m)return;
if (!step)
{
Hash(u, S, dist);
return;
}
for (int i = 1; i < n; i ++)
{
if (S & bit[i])continue;
dfs1(step - 1, i, S | bit[i], dist + w[u][i]);
}
}
void dfs2(int step, int u, int S, LL dist)
{
if (dist > m)return;
if (!step)
{
res += get_hash(u, (((bit[n] - 1) ^ S) | bit[u]) | 1, m - dist);
return;
}
for (int i = 1; i < n; i ++)
{
if (S & bit[i])continue;
dfs2(step - 1, i, S | bit[i], dist + w[u][i]);
}
}
int main()
{
freopen("way.in", "r", stdin);
freopen("way.out", "w", stdout);
scanf("%d%d", &n, &m);
bit[0] = 1;
for (int i = 1; i <= n; i ++)bit[i] = bit[i - 1] << 1;
for (int i = 0; i < n; i ++)
{
for (int j = 0; j < n; j ++)scanf("%d", &w[i][j]);
}
dfs1(n >> 1, 0, 1, 0);
dfs2(n - (n >> 1), 0, 1, 0);
printf("%d", res);
return 0;
}