早上8:00,我们来到了这与我们真正“亲爱”的Quanzhou No.1 High School。开始了一整天的集训。
上午
打比赛——【CSP2025】初二寒假集训day3-0122
(It is a little hard.)
So I hope tomorrow’s test will be simpler.
成绩 290/500(second)
T1(100 -> 100)

这是一道很简单的题目
赛时思路:
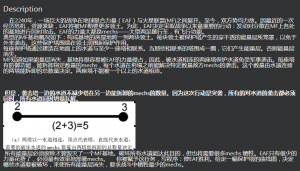
1.容易想到答案为两个点所在圆的数量的和
2.代码实现时如果一个点在圆内,则f[i]=!f[i]
这是以免出现两个点在同一个圆内,而答案有+1的情况
(如下图所见)
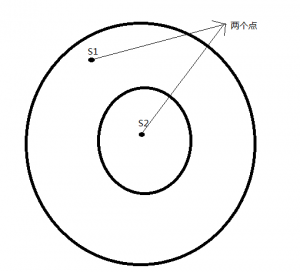
赛时代码:
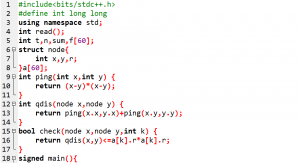
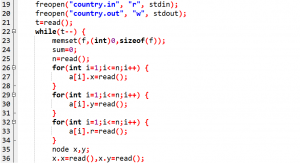
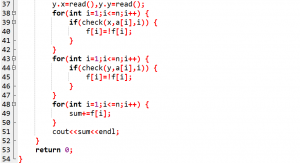

T2(没打 -> 没打)

这是一道很“简单”的题目
赛时思路:
没打
赛时代码:
没打
标程思路(由ymh提供):
注意到这一题其实可以构建图论模型
1.小跳跃是没有代价的,而且小跳跃之后所在节点奇偶性不变。
2.由于每个洞是不能进入的,所以可以把每段可以走的路作为节点,再把这个节点拆成两个点,其中一个表示这段能走的路的奇数点,另一个表示偶数点。
3.然后枚举每对节点,如果可以从i节点大跳跃到j节点,则连边。
4.最后求一次最短路(由于是不加权的图,用bfs就可以了)
标程代码:
没打,就不放了
T3(100 -> 100)
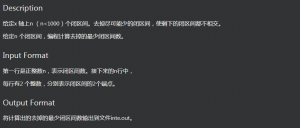
这是一道很简单的题目
赛时思路:
dp解决
1.容易想到求去掉的最少闭区间数=总数–求保留的最多闭区间数
2.dp[i][j]表示在前i个中,一定要取第j个的最多闭区间数
3.状态转移方程:
(1)if(a[k].y<a[j].x)
dp[i][j]=max(dp[i-1][j],dp[i][j],dp[i-1][k])
(1<=k<=j-1)
(2)else
dp[i][j]=dp[i-1][j]
赛时代码:

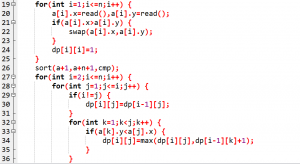
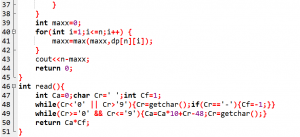
标程思路(由ymh提供):
贪心算法
1.策略是在可选区间中选右端点最小的,右端点越小,之后可选的区间越多。
2.所有区间按r[i]排序。
好处:
(1)首先可以去除区间包含的情况(只留小区间)。
(2)此时的l[i]同样是有序的。
3.考虑前两个区间,若不选第一个区间,则相当于[l[1],l[2]]这段区间无用。(此时也是种包含情况,选第二个不会更优)
标程代码(由lft提供):
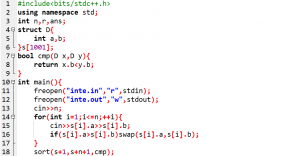

T4(10 -> 60)

这是一道稍微“简单”的题目
赛时思路:
骗分
赛时代码:
骗分
标程思路:
容易想到答案为每条边的权值之和–在每个连通块中求最大生成树的权值之和
标程代码(由伟”栓”独家提供):
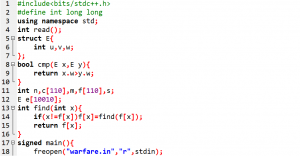
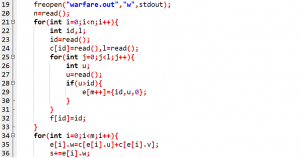
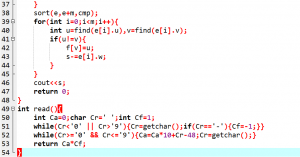
T5(80 -> 100)
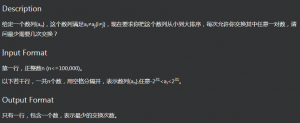
这是一道稍微简单的题目
赛时思路:
暴力(得了80分!!!数据太水了)
赛时代码:
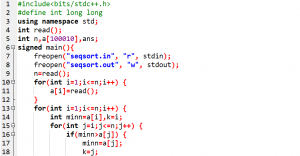

标程思路(由ymh提供):
因为每一个数都有一个属于自己的最终位置,所以我们让每一个数换到它最终的位置之后,它就不用再动了。(也就是每个数换一次。)
标程代码:
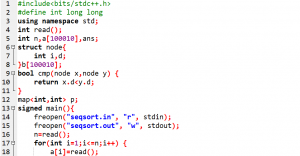
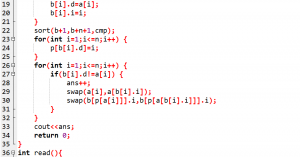

下午
改题,听课(讲了最小生成树和拓扑排序),打题
最小生成树
概念:
最小生成树也叫最小代价树,对于一个带权连通无向图G=(V,E),生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spanning-Tree,MST)。
Kruskal算法(加边法):
思路:
每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选了,可以用并查集维护),直到所有节点都连通。
模版题
主要思路:
1.输入边,用结构体储存
2.用结构体快排以边比较从小到大快排
3.建一个并查集,并初始化并查集(并查集代表两个点有没有在同一个树里面)
4.设边edge[100000],edge.start一个点,edge.to另一个点,edge.val是边长,ans是最终答案。
5.从1-m中找一条边edge[i]
(1)若edge[i].start与edge[i].to不在同一个并查集里面,就将edge[i].start与edge[i].to所在的并查集合并,并将ans+=edge[i].val。
(2)若在同一个并查集,则跳过这次循环。因为如果这两个点连接起来,就会形成一个环。
代码:
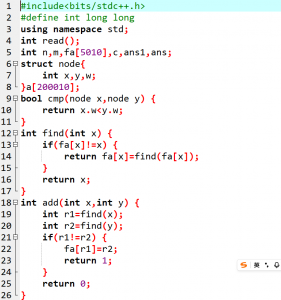
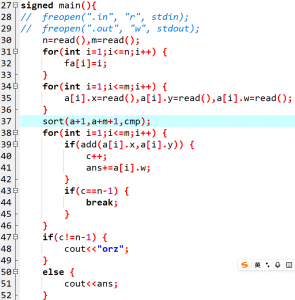

prim算法(加点法):
不常用,就不介绍了
拓扑排序
概念
拓扑排序是一个有向无环图的所有顶点的线性序列。
该序列需要满足每个顶点出现且只出现一次和如果有一条A到B的路径,在序列中A出现在B的前面。
模版题
主要思路:
1.计算每个点的入度。
2.入度为0就加入队列。
3.当队列不为空则循环:
(1)取出队首元素并输出。
(2)遍历队首元素的连边,对应节点的入度−1。
(3)当对应的节点入度为0就加入队列。
代码:
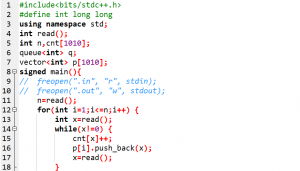
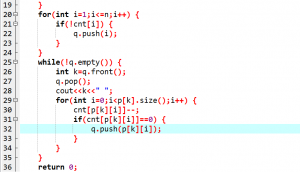
晚上
改题,打题,写博客