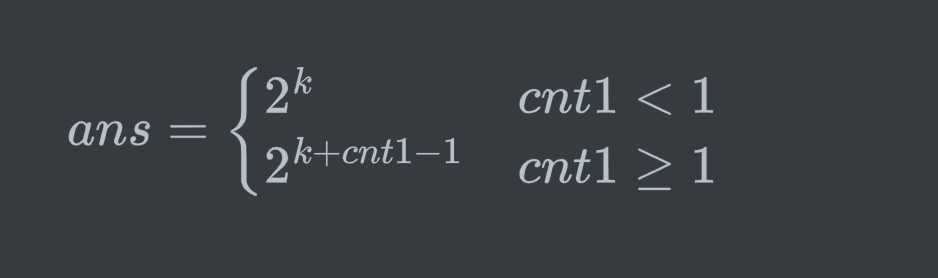长乐集训Day?（貌似已经进行好几天了）.1

————我真的会谢

上午

只有T1

简化（也没简多少）一下题意：

1. 给定一个长度为 n 的正整数序列 \left\lbrace a_i\right\rbrace 。
2. 将这个序列分为两个非空序列 \left\lbrace s_i\right\rbrace 和 \left\lbrace t_i\right\rbrace。
3. 要求 \operatorname{gcd}(\prod s_i ,\prod t_i )=1 （s中各个元素的乘积与t中各个元素的乘积的最大公因数为1）。
4. 问：有几种划分方式，答案对10^9+7取模。

思路+调试过程（谢的过程）：

为了保证最大公因数为1 ，所以对于任意的s_i和t_i的最大公因数只能为1 ，也就是它们不能有除了1以外的任何公因数，于是我么就可把这些数分类，把拥有相同因数（相同因数不包括1，否则所有数都在一起了）的数字划分到同一组，这个过程就可以用并查集来实现了（比赛的标题就是并查集） ，划分完组后就可以把这几个组随意放置（因为两个组的任意数之间没有除1的公因数，所以可以乱放，也就是放在s或t都可以，可以保证题目要求的条件），然后就回到组合数学了，假设这些数被分成了k 组，那么答案就是 2^k （可以理解为把k个物品放到两个箱子里，问有几种方法），通过快速幂求解。

至于分组部分，我们可以先把每个再a中的数用桶排标记了，再用线性筛素数把10^7内的所有素数筛出来，然后暴力枚举每个prime_i\times j (prime_i\times j \le \operatorname{max}(a_i))，如果prime_i\times j属于a ，那么就把prime_i\times j和prime_i 用并查集合并到一起，最后再来暴力遍历 a_1~a_n统计有几组。

完成！

这真的完了吗？答案是还没，我们没有考虑a中有1的情况，因为1不会影响两个序列中各个元素的乘积，所以放哪里都可以也就是把每个1看成单独的一组，所以答案是2^{k+cnt1} ，cnt1是a中1的个数。

好吧，其实应该是这样：

好啦，这题就完了。

这真的完了吗？当然没有，s和t非空，但答案却把它俩为空的情况算进去了，所以实际上答案应该是：

真的完了。

代码：

#include<bits/stdc++.h>
#define LL long long
#define MAXA 1000010
using namespace std;
LL mod=1000000007;

int p[MAXA];
int find(int x)
{
    if(p[x]==x) return p[x];
    return p[x]=find(p[x]);
}
void merge(int x,int y)
{
    int xx=find(x),yy=find(y);
    if(xx!=yy) p[xx]=yy;
}

LL power(int x,int y)
{
    LL ret=1LL,tmp=(LL)x;
    while(y>0)
    {
        if(y&1)
        {
            ret*=tmp;
            ret%=mod;
        }
        tmp*=tmp;
        tmp%=mod;
        y>>=1;
    }
    return ret%mod;
}

int cnt,v[MAXA],prime[MAXA];
void primes(int n)
{
    for(int i=2;i<=n;i++)
    {
        if(v[i]==0)
        {
            prime[cnt++]=i;
            v[i]=i;
        }
        for(int j=0;j<cnt;j++)
        {
            if(prime[j]>v[i]||prime[j]>n/i) break;
            v[i*prime[j]]=prime[j];
        }
    }
}

void aha()
{
    int n,xi=0,ct1=0,ma=0,a[100010];
    bool fg[MAXA],tg[MAXA];
    memset(fg,false,sizeof fg);
    memset(tg,false,sizeof tg);
    cin>>n;
    for(int i=1;i<=1000000;i++)
    {
        p[i]=i;
    }
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        ma=max(ma,a[i]);
        fg[a[i]]=true;
        if(a[i]==1) ct1++;
    }
    for(int i=0;i<cnt;i++)
    {
        for(int j=1;j*prime[i]<=ma;j++)
        {
            if(fg[prime[i]*j])
            {
                merge(prime[i],prime[i]*j);
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        int tmp=find(a[i]);
        if(!tg[tmp])
        {
            tg[tmp]=true;
            xi++;       
        }
    }
    if(ct1>=1) ct1--;
    cout<<(power(2,xi+ct1)-2ll)%mod<<endl;
    return;
}

int main()
{
    primes(1000000);
    int T;
    cin>>T;
    while(T--)
    {           
        aha();
    } 
    return 0;
}

但是，细心的同学一定会发现这份代码会爆零。

死因：没有文件读写

真的折磨了我好久，从莫名其妙地爆零到想要测试一下大样例才恍然大悟。

下午

只有T1

这题只要稍微思考一下就知道是要求最小生成树。按理说很简单，结果写炸了，关键是不知道为什么炸了，很谢。

总结：今天大部分时间都在调 A. 集合划分 ，大概就是编译器坏了不可以调试，然后上网又下了一个，结果点错了，带了一堆软件，接着又是细节和文件读写。OJ有点卡测评要等上好一会儿。