早上8:00整,我们又又又来到了这与我们“亲爱”的Quanzhou No.1 High School有长达20个英文字符的最长公共子序列的Changzhou No.1 High School。
上午
讲了各种树
树
树是一种非线性的数据结构,用它能很好地描述有分支和层次特性的数据集合。
先序遍历
先序遍历是先访问根结点,再从左到右按照先序思想遍历各棵子树。
后序遍历
后序遍历是先从左到右遍历各棵子树,再访问根结点。
层次遍历
层次遍历是按照层次从小到大逐个访问,同一层次按照从左到右的次序访问。
叶结点遍历
有时把数据信息存放在叶结点中,其余结点都是用来表示数据之间的某种分支或层次关系。这种情况下只需要访问所有的叶结点,此时就采用叶结点遍历法。
二叉树
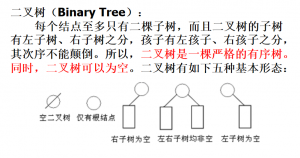
相关性质
(1)二叉树的第i层上至多有2^(i-1)个结点(i≥1)。
(2)深度为k的二叉树至多有2^k –1个结点(k≥1)。
满二叉树
一棵深度为k且有2^k –1个结点的二叉树,称为“满二叉树”。
完全二叉树
在满二叉树的基础上,在最后一层的最右边去掉几个连续的节点,称为“完全二叉树”
二叉树的遍历
先序遍历
若二叉树非空,则先访问根结点,再分别先序遍历左子树和右子树。
中序遍历
若二叉树非空,则先中序遍历左子树,再访问根结点,最后再中序遍历右子树。
后序遍历
若二叉树非空,则后序遍历左子树,再后序遍历右子树,最后访问根结点。
下午
优先队列
容器
容器默认为vector。
比较方式
比较方式默认为
bool operator<(int x,int y)
{
return x<y;
}
大根堆
priority_queue<int> q;
小根堆
priority_queue<int,vector<int>,greater<int> > q;
常用代码
q.push(x) 插入一个数
q.top() 取队首
q.pop() 队首出队
q.empty() 判断队列是否为空
二叉堆
二叉堆是一种常用的优先队列,它支持优先队列的三个基本操作,且插入结点和删除最小结点的时间复杂度都是O(log2n),取最小结点的时间复杂度是O(1)。而且编程简单,效率高。
哈夫曼编码与哈夫曼树
构建方式(哈夫曼算法)
具体做法是:
(1)根据给定的n个权值{W1,W2,…,Wn},构造n棵二叉树的集合 F ={T1,T2,…,Tn},其中每棵二叉树均只含一个权值为Wi的根结点,其左、右子树为空树;
(2)在F中选取其根结点的权值最小的两棵二叉树,分别作为左、右子树构造一棵新的二叉树,并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和;
(3)从F中删去这两棵树,同时加入刚生成的新树;
(4)重复(2)和(3)两步,直到F中只有一棵树为止。
并查集
概念
并查集(union-find set)是一种用于分离集合操作的抽象数据类型。它所处理的是“集合”之间的关系,即动态地维护和处理集合元素之间复杂的关系,当给出两个元素的一个无序对(a,b)时,需要快速“合并”a和b分别所在的集合,这其间需要反复“查找”某元素所在的集合。“并”、“查”和“集”三字由此而来。在这种数据类型中,n个不同的元素被分为若干组。每组是一个集合,这种集合叫做分离集合(disjoint set)。并查集支持查找一个元素所属的集合以及两个元素各自所属的集合的合并。
并查集支持的操作
MAKE-SET(x)
建立一个新的集合,其仅有的成员(同时就是代表)是x。由于各集合是分离的,要求x没有在其它集合中出现过。
UNION(x,y)
将包含x和y的动态集合(例如Sx和Sy)合并为一个新的集合,假定在此操作前这两个集合是分离的。结果的集合代表是Sx∪Sy的某个成员。一般来说,在不同的实现中通常都以Sx或者Sy的代表作为新集合的代表。此后,由新的集合S代替了原来的Sx和Sy。
FIND-SET(x)
返回一个包含x的集合的代表。
题目
亲戚

思路
并查集基本模板,十分简单,就不讲了。
代码
#include<bits/stdc++.h>
using namespace std;
int fa[20010];
int m,n,i,x,y,q;
int find(int x)
{
while(fa[x]!=x)
{
x=fa[x];
}
return x;
}
void fun(int r1,int r2)
{
fa[r2]=r1;
}
int main()
{
cin>>n>>m;
for(i=1;i<=n;i++)
{
fa[i]=i;
}
for(i=1;i<=m;i++)
{
scanf("%d%d",&x,&y);
int r1=find(x);
int r2=find(y);
if(r1!=r2)
{
fun(r1,r2);
}
}
cin>>q;
for(i=1;i<=q;i++)
{
scanf("%d%d",&x,&y);
if(find(x)==find(y))
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
return 0;
}