上午打题

今天依旧没有比赛，打之前没打完的题

T1

昨日的比赛第二题

这里的话首先注意到模数100003是一个质数（看完标程后又自己试验了一下发现的），因此计算乘法逆元时，我们可以用费马小定理帮助求解
接着看到有8个点(40pts)是所有询问均是求解第m行之和
那么我们先考虑这个询问

一件显然的事情，第m每个数都能被分解成上一行的数分别与B，C相乘后除以A的形式，那么显然最后的结果应当是（B+C）/A倍的上一行的乘积

那么容易得出第m行的和应为(（B+C）/A)^m
这里用快速幂即可

而另外的询问与组合数有关，我们可以预处理阶乘，然后使用卢卡斯定理

具体推导过程看题解

欧拉筛

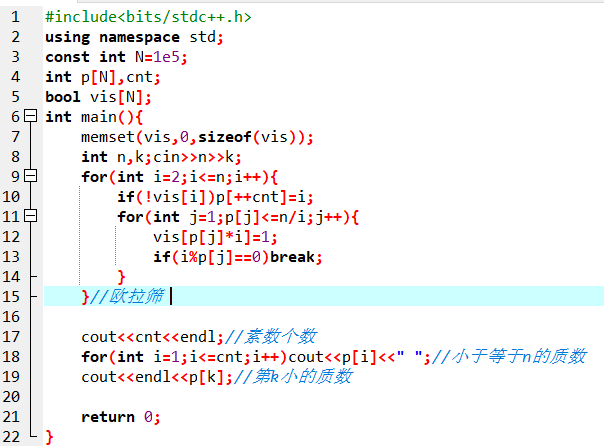
算法复杂度是线性的，因为欧拉筛保证每个数只被扫描一次，均摊后复杂度是O(n)

应用：质数个数————from qz1zOJ

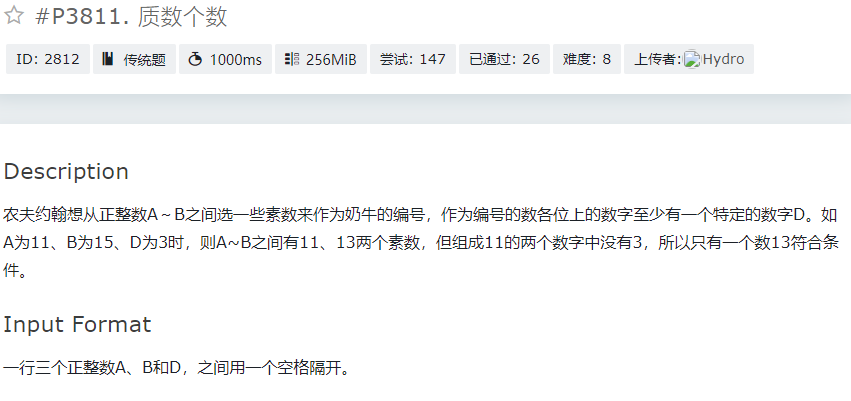
首先看一下数据范围

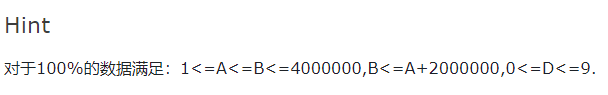
显然不能使用逐个判断素数的方法，极限情况下会超时，因此我们可以想到的是埃氏筛或欧拉筛

这题埃氏筛也能过，但是我们还是使用欧拉筛来做这题

T3

这题实在逆天，考了图论和贪心

看题解吧

神奇思路
这段代码主要的编写难度在于状转的部分是否可以想到

下午背包问题

下午讲了背包的几种不同的题型以及优化
然后还是没开网，然后就在泉一OJ上自己打题

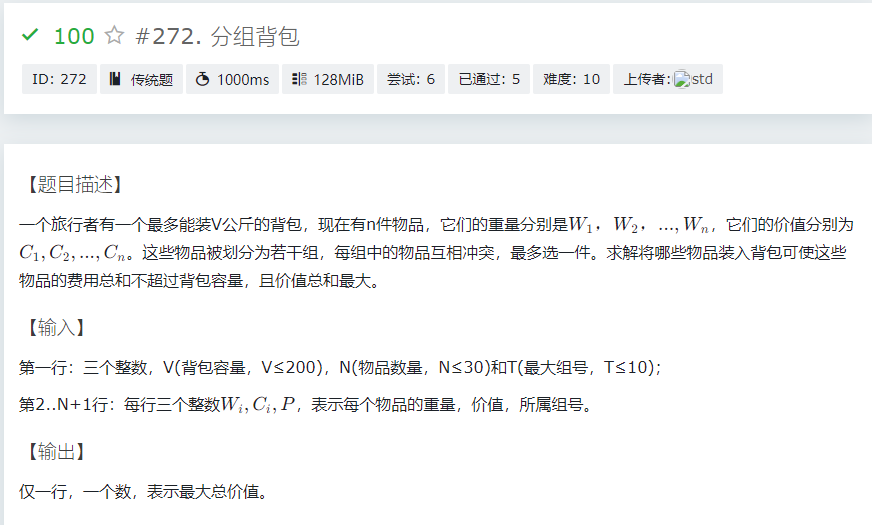
可以看出我们无法像之前做01背包时直接枚举每一个物品，这是因为这题中，物品与物品之间相互牵制，有排斥，所以我们应当按题目要求进行分组，然后再做01背包

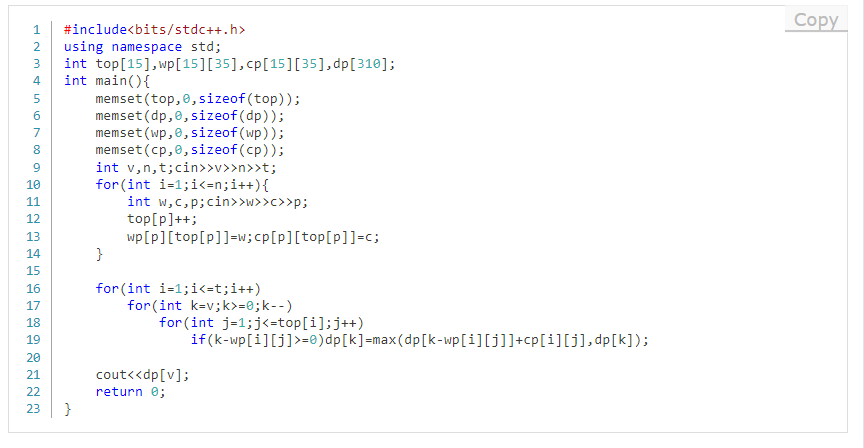
晚自习

打背包题

T1

纯纯01背包，一道水题

T2

依旧水题一道，裸01背包

T3

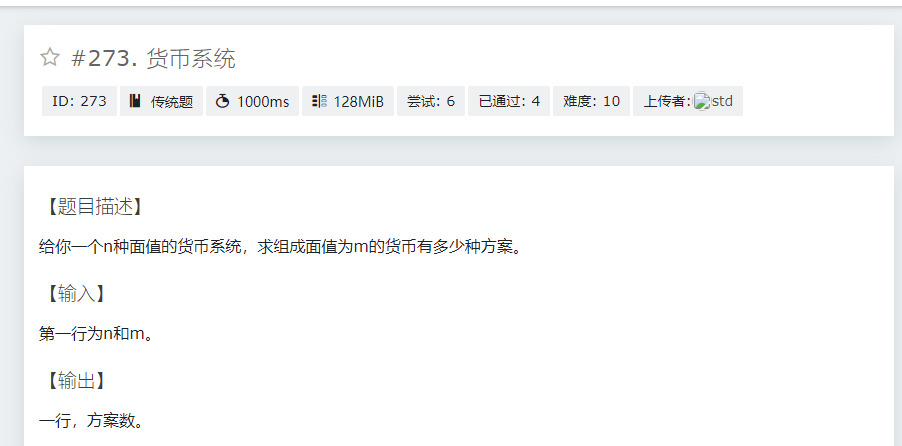
这题看起来与背包毫无关系，实际上，题目中隐含的条件是：
背包容量为m，每个货币所占空间与权值均为它本身，且所有货币均有无限个

这样就转换成了一道背包题目，而这道题与以往不同的是，要求的是可以获得m权值的方案数，转化一下，就是说相当于求最优方案的总数

那么考虑用一个新的数组来存储方案数，假设g[i][j]表示选取第i件物品时,占用j空间的方案数
已知背包的状转方程是dp[i][j]=max(dp[i-1][j],dp[i][j-v[i]]+w[i])
那么最优方案就是从g[i-1][j]和g[i-1][j-v[i]]转移的

那么当dp[i][j]=dp[i-1][j]时，g[i][j]+=g[i-1][j]
当dp[i][j]=dp[i-1][j-v[i]]+w[i]时，g[i][j]+=g[i-1][j-v[i]]

那么考虑优化空间，将第i维省去，就有以下代码

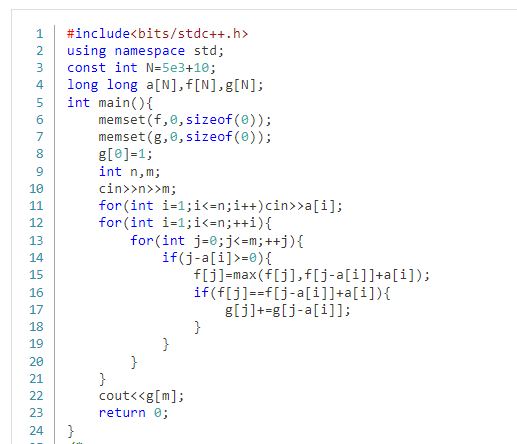
T4

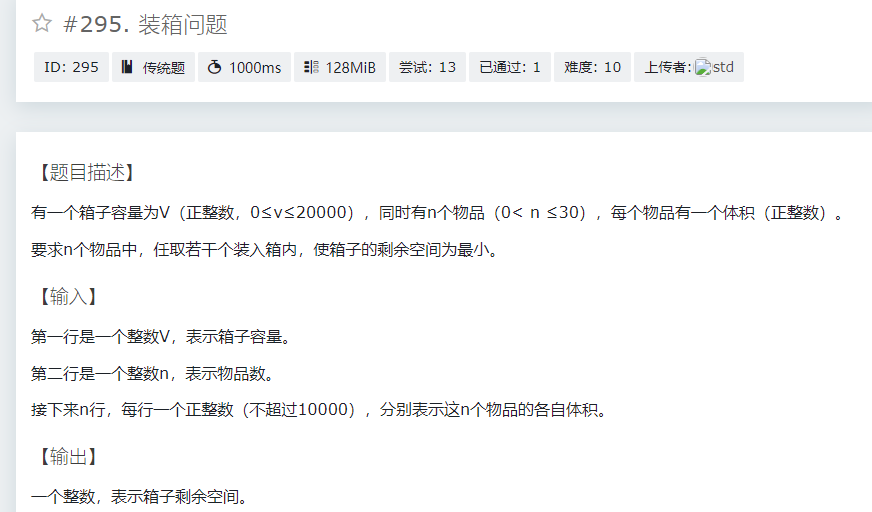
仍然01背包，注意最后的输出是输出剩余空间

T5

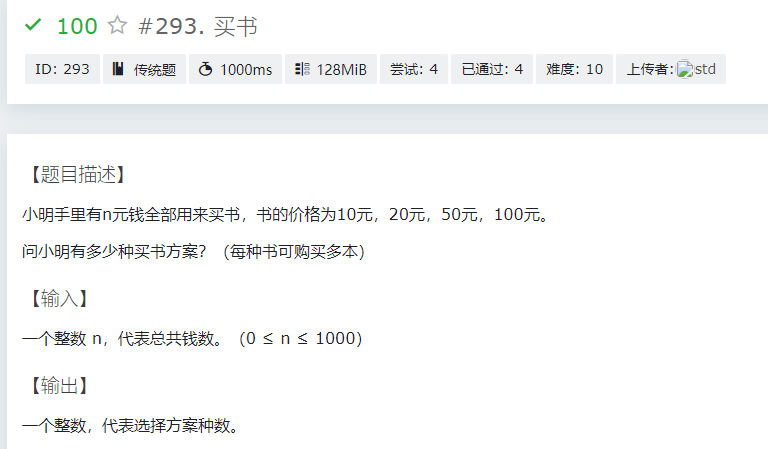
这题也需要一点转换，就是将背包容量当作n,物品的空间与权值就是题目中给定的10，20，50，100
这题仍然求的是方案数，那么思路与T3相同，不做过多赘述

T6

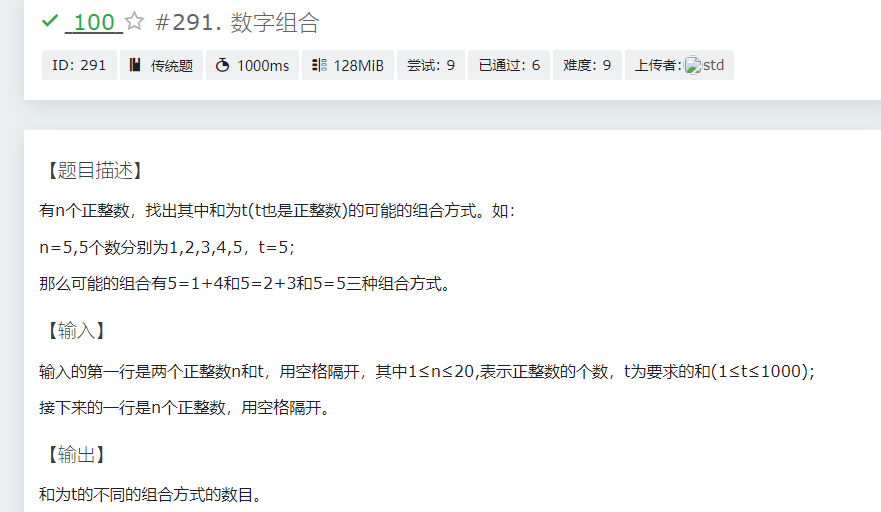
与T5和T3相似，唯一不同的是这里是01背包而不是完全背包