上午比赛
今天比赛打了95分,第一题没看懂题目样例是怎么算的,就没打,后来赛后交流时才弄懂,结果发现那题竟然很简单
下午数学
这次课直接一节课讲了在聚龙讲了好几节课的东西,把组合数学和数论都大部分讲完了,讲得很快,还好已经学过了
老师没开网,上不了洛谷打题,只能改改早上比赛题
晚自习
改上午比赛题
T1

这题早上的时候由于不知道样例是怎么计算的,于是就没打了
所以晚上先补一下这题
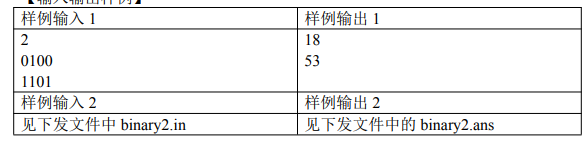
首先说明一下,以这个样例中第一个序列为例
0100
可以被拆作0,1,0,0,01,00,00,10,10,00,010,010,100,0100
这几个子序列,上午的时候由于没有考虑到子序列不一定连续,而忽略了一些对答案有贡献的,导致无法做题
那么回到题目,我们可以按位考虑在各个位上的“1”,对答案的贡献
容易发现如上面0100的序列就是一个很好的例子,便于我们研究单个“1”的贡献
在第2位上的“1”,可以最大表示的是2的2次方,即在100或0100这个子序列中,最小的可以表示为1,即在01或1的子序列中,可以看得出来,其对答案的贡献是与其所在的位置有关的
再来看一下其在子序列中在第2位的情况
010,010
由乘法原理可以得到位置与贡献的关系
然后我们需要预处理,避免超时问题
Code1
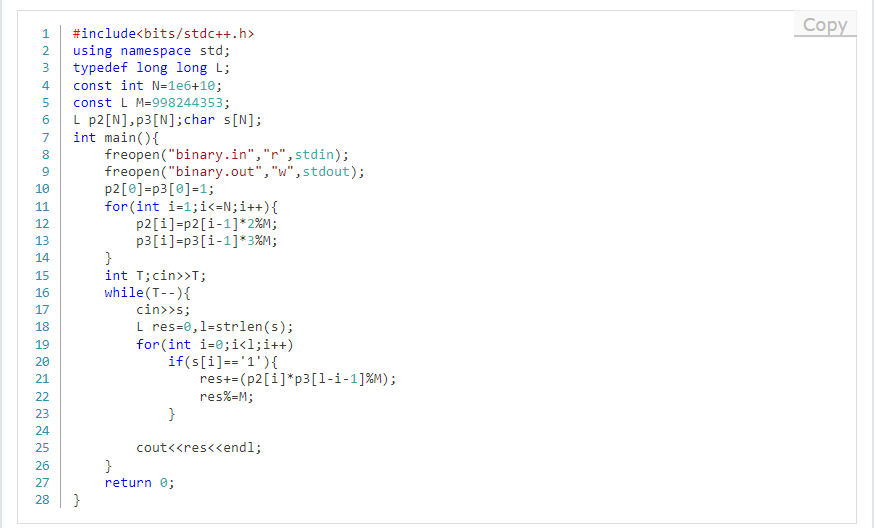
T2

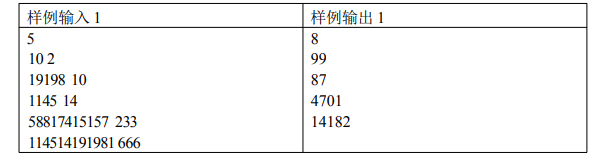
首先注意到样例非常的臭(bushi
首先我们可以注意到题目显然是要我们求解存在多少个w能使得n%w<=k
那样我们不妨设n=aw+b
那么n%w=b=w=(n-b)/a>=(n-k)/a这样可用于确定b的范围进行判断
因为模运算是构成环的,所以我们不必每一次都枚举符合条件的w,我们可以用分块的思想设定某个值,在小于等于这个值时考虑枚举w,大于时枚举a,这样就能扬长避短,减少消耗的时间,通过这题
设临界值为s
这里我们计算时间复杂度 容易得到总复杂度为O(n/s+s),根据基本不等式,当s=sqrt(n)时,有最值
所以我们要确定的临界值就为sqrt(n)
AC代码如下
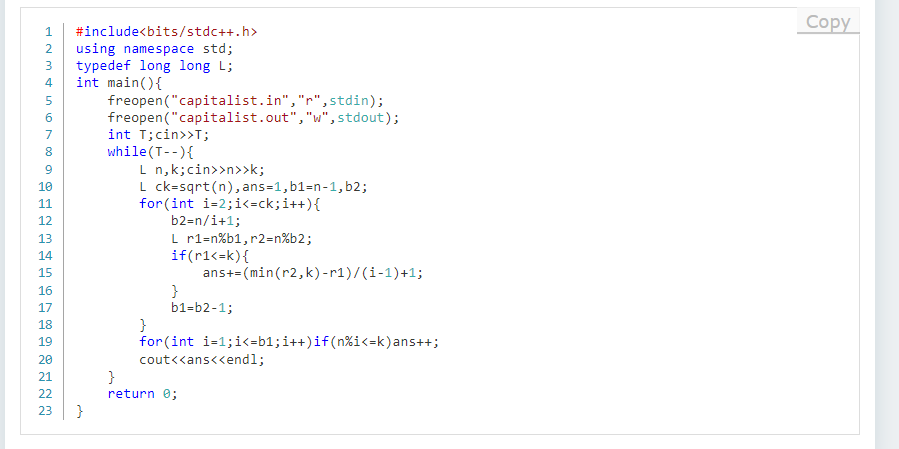
今天day5