上午打题

今天没比赛，早上打之前没打完的题目

T1

这是比赛题
注意到这些数字的位置变换符合环
这题核心思路是找环，通过环的长度来判断还原当前这个环需要的最短步数

注意到当环的长度小于等于4时，可以一次复原，但是要特别注意，当有2个长度为2的环时，它们可以一起复原，因此对长度为2的环要特判，用一个变量来存储有多少个长度为2的环

同时当环的长度大于4时，一次机会最多复原3个数字位置，因此可能会出现只剩两个数字未被复原的情况，这里我们将环的长度对3取模，那么若余数等于2，就把它当作环长为2的小环，对其进行计数

然而许多人都会拿到90分的高分，因为超时，然而算法无法优化，只能通过优化常数的复杂度拿到100

AC代码如下

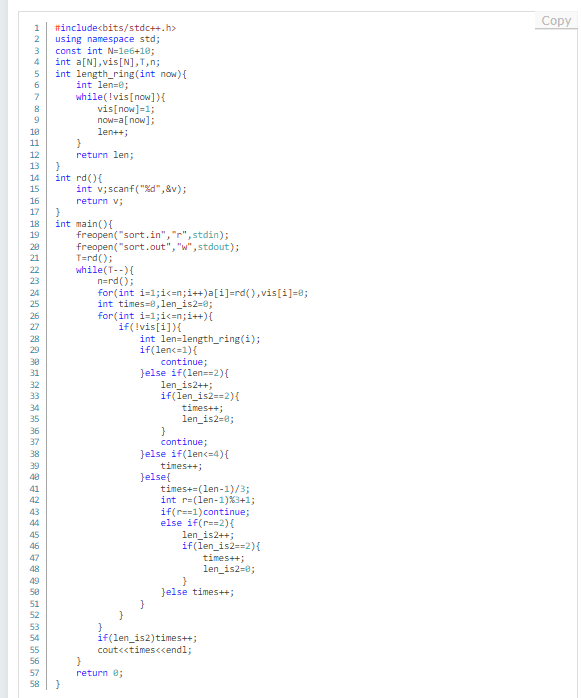
这里我将定义变量、输入和清空vis数组的常数优化了（之前每次循环都定义了变量，又额外用memset()函数清空vis数组，还有用cin进行读入）

优化后运行时间相当优秀

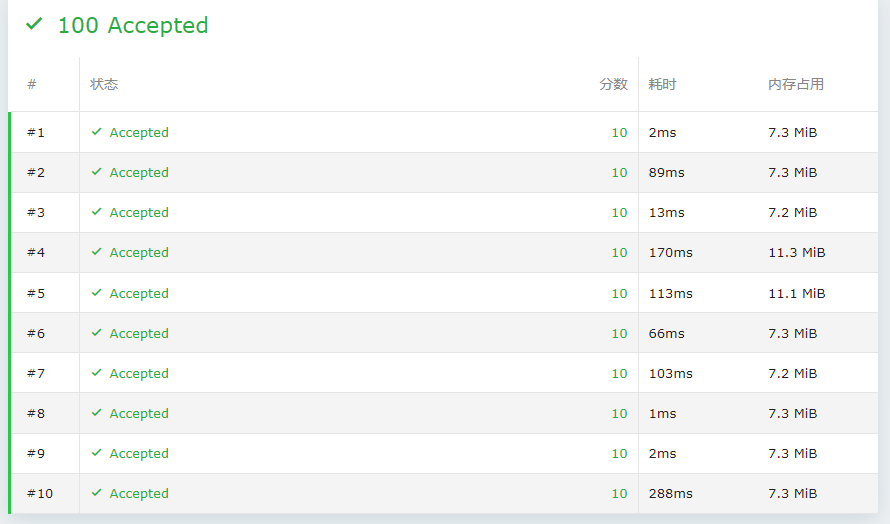
不优化的话有一个点会爆TLE（别问我是怎么知道的）

T2

这题需要用一点点物理小知识，由于光路可逆，因此当以相同的方向经过同一面镜子时，会重复走相同路径

这时就又涉及到环

容易发现，一束光线若以固定方向所走的路径必然在环内或不在环内
我们进行特判

若在环内，这束光必然会重复以相同方向经过同一面镜子，若是这样，则返回
若不在环内，这束光将会出界，就要判断是否出界

我们可以用dp[x][y][z]来表示在镜子(x,y)处以z方向行进，会到达的不重复镜子数，这样可以用记忆化的思想进行优化，无需每次都遍历路径，若当前路径已被走过那么就直接输出当前的编号dp，O（1）即可完成，这样就避免了超时的问题

首先我们从边界开始枚举从上往下、从下往上、从左往右、从右往左扫一遍，找到会出界的路径，记录出界路径中，每个点可以到达的点数，这么做是可行的，因为光路可逆，实际上就是在找路径为链的路径

然后按照题目读入测试数据，判断当前点的前进方向是否曾经遍历过，如果有，直接输出即可，没有的话，那就是在整个图中，这个点应该在没有触碰到边界的环内

当然我们可以把用于标记的数组和dp数组用同一个，以节省空间

还有判重问题，我们可以用std::set来删去重复的经过的点，方便代码书写

整体的时间复杂度应该是O（4mn）省去4得O(mn)

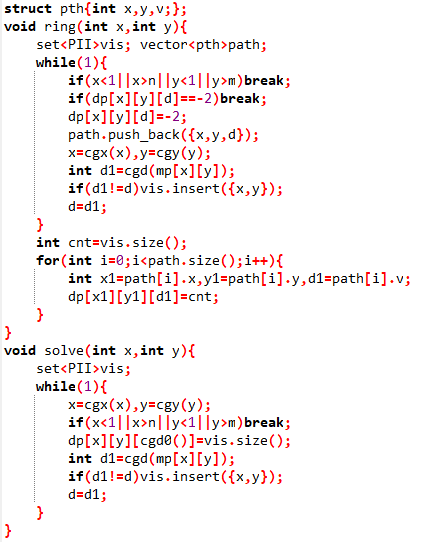
代码太长就不放了(再压缩代码行数就不礼貌了),放一下核心代码（100行的代码，实在截不了图，用这里的代码板块又容易被吃掉字符（建议修复一下！！！！））

以下d=1,2,3,4分别表示当前方向是上、下、右、左

下午：二分答案

若遇到题目中，有将最大值最小化或最小值最大化的字眼，可以考虑二分答案

以下是自己在洛谷打的题

一元三次方程求解

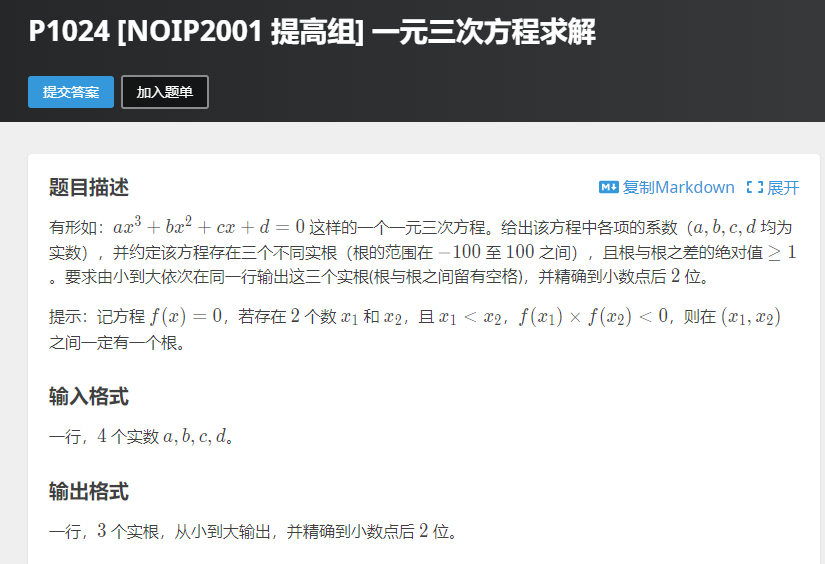
观察三次函数图像，可以看出当函数在x轴时有三个交点时（即有三个根时），其中中间的根必然在两个极值点之间，我们可以通过求导，求出极值点的横坐标

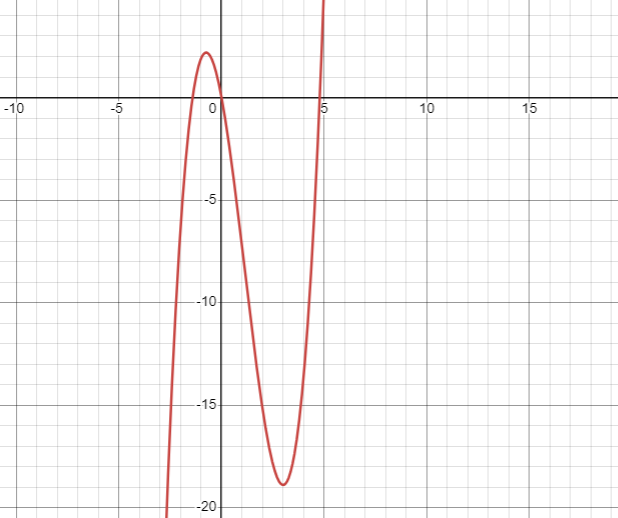
就是令f(x)=ax^3+bx^2+c^x+d
则f'(x)=3ax^2+2bx+c
令f'(x)=0，求得的两个解就是极值点的横坐标

用二分法就可以找到最中间的根
至于剩下的两个根，根据题目条件我们知道
x1的范围是【-100，x2-1】
x3的范围是【x2+1,100】
根据范围二分查找即可

AC代码如下

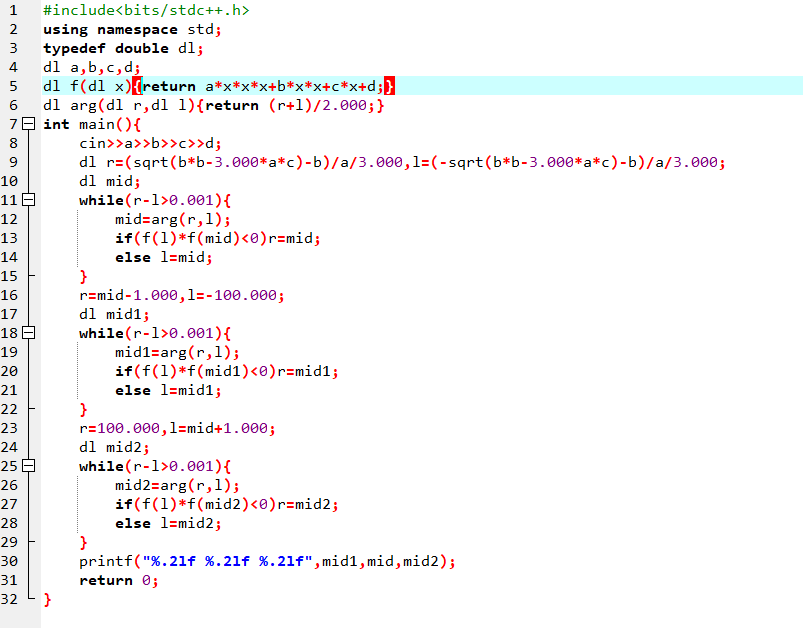
然后看到洛谷题解里求根公式、牛顿迭代法各种非二分方法层出不穷，好好一道二分题，整出了O(C)的解法，实在逆天
当然，这题我本来想做完中间根的查找后，用三次韦达定理，转化为一元二次方程，再套求根公式求解的，但是后来一想可能精度会不够，索性没打了

跳石头

好，这题显然我们得用终极大法——题解法来解决
看大佬的思路

好吧，纠正一下，题目已经给定按从小到大顺序给出石头到出发点距离我们没必要在进行排序了

我们可以看出题解的思路是先假设了一个需要最大跳跃的最小距离，然后，用二分的方式，判断当前跳跃距离是否满足题目的条件，即移走的石头数小于等于M，若满足，则当前的跳跃距离一定目前是最优的，所以当while循环停止时，我们可以求得最终的答案

于是我们二分查找最大跳跃的最小距离
AC代码如下

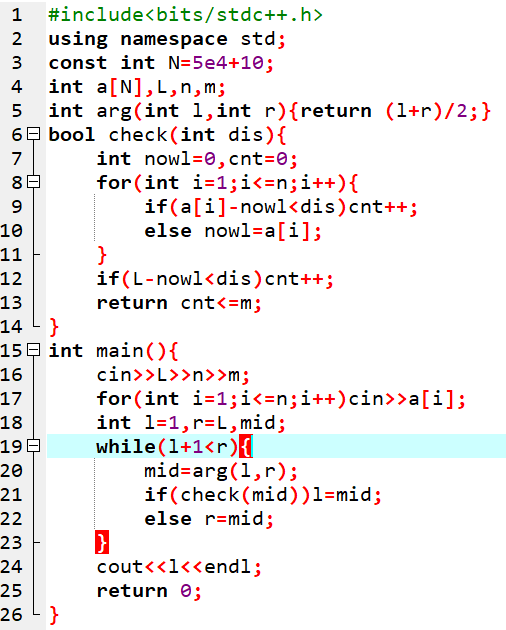
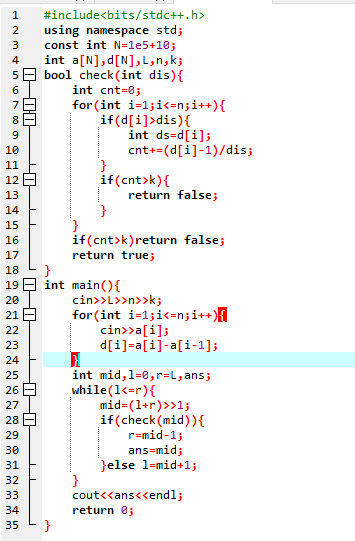
路标设置

不知道为什么第一个点RE

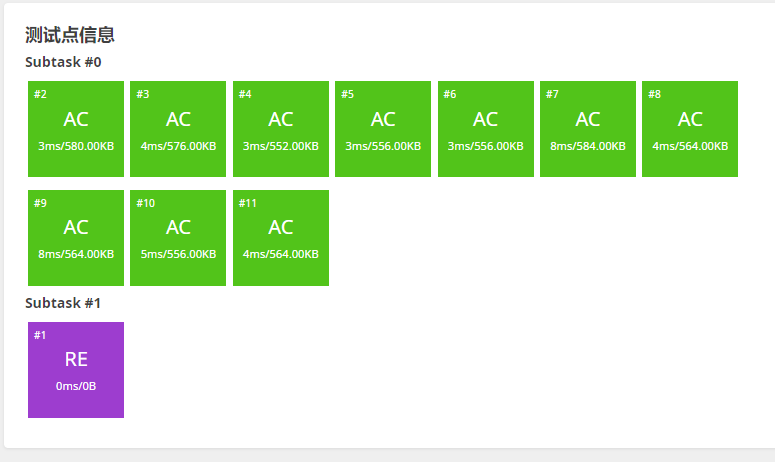
求调

晚自习

无