电脑死机了2次了，这是我第n次打这篇blog，已老实，求放过:sweat_smile: :sweat_smile:

图的连通性问题

今天我们学习了图的连通性问题，学到了很多新的概念，比如：割点、割边（桥）、点双连通图、点双连通分量、边双连通图、边双连通分量、强连通分量……

还学习了Tarjan算法，用于求解割点、桥等连通问题

练习题

炸铁路

显然是让我们求解图中的所有桥，并且按字典序从小到大输出

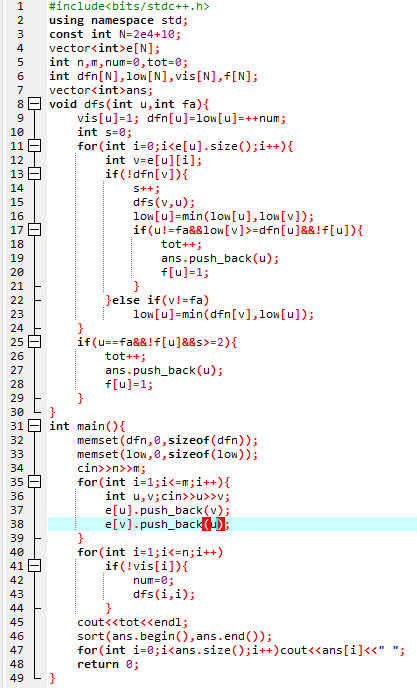
我们可以用Tarjan算法求解桥，但是，在实践时，我遇到了一个问题，老师的PPT中，模板中存图方式用的是链式前向星，但我不会，因此只能将其转换成vector形式的模板
因此经过一场头脑风暴后，我成功写出了用vecotr存图版本的Tarjan算法模板
然而，又很容易想到最后的答案可以用vector的形式存储，用sort排序输出
所以一个“伟大”的代码诞生了

割点

原谅我的截图技术，我少截了一段信息

题目所给的图不一定连通

也就是说，题目给的可能是很多个图的集合

因此我们应当以每一个未被遍历的点作为源点遍历图，确保每个点都被遍历过

我们可以用一个for来循环源点然后跑多次Tarjan

这样就能AC

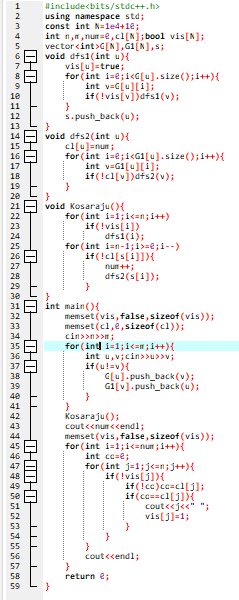
Kosaraju算法

在OI_Wiki上看到求强连通分量的算法
代码量竟然这么小！
到百度上一搜发现时间复杂度除了常数大一点之外，和Tarjan差不多，只弱了一点点，必须安利一下

其核心思想是跑两边dfs，一次正图，一次反图
例题

极限拿捏

LAST

这大概就是我为么今天电脑死了两次机，我打了三遍这篇博客的原因吧:sweat_smile: