GDNOJ-DAY 4

Posted on By 张, 高畅 GDNOJ-DAY 4无评论

你猜有没有密码？

算了不玩了

神奇的数学题，实在是太……不好玩了

这简直是奇耻大辱

[A]

原题(easy ver.)

首先整理一下式子：

$\frac{1}{x}+\frac{1}{y}=\frac{1}{n!}$

很显然由于 x>0 且 y>0，因此 \frac{1}{x}>0，\frac{1}{y}>0

所以 \frac{1}{x}<\frac{1}{n!}，\frac{1}{y}n! 且 y>n!

不如设 y=n!+k (k>0)

有 \frac{1}{x}+\frac{1}{n!+k}=\frac{1}{n!}，通分后得：

$x \cdot k=(n!)^2+n!k$

所以 x=\frac{(n!)^2+n!k}{k}，即 x=\frac{n!}{k}+n

因此我们其实就是要求 (n!)^2 的因数个数。

我们考虑将 (n!)^2 分解质因数，这样假设最终分解的结果为 $p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdot … \cdot p_k^{\alphak}，那么答案即为\prod{i=1}^{k} (\alpha_i+1)$

因此我们将每一个 i (1 \leq i \leq n )分解质因数计算答案就可以了。

时间复杂度取决于实现，注意hard ver.需要使用一个trick：由于高精度乘法的复杂度较大，因此可以设一个中间变量 tmp，让 tmp 先去乘上 \alpha i，直到 tmp 快要爆炸的时候再进行高精度乘法。

CODE(easy ver.)

#include
using namespace std;
typedef long long LL;
const int N=1e6+5,mod=1e9+7;
int primes[N],cnt,st[N];
void init(int n)
{
    for(int i=2;in;
    init(n);
    int res=1;
    for(int i=0;i<cnt;i++)
    {
        int p=primes[i],s=0;
        for(int j=n;j;j/=p)s+=(int)j/p;
        res=(LL)res*(2LL*(LL)s+1LL)%mod;
    }
    cout<<res;
    return 0;
}

CODE(hard ver.)

#include
using namespace std;
const int N=7e5+5;
const int base=1e9;
typedef long long LL;
LL n,primes[N];
int st[N],p[N],cnt;
inline vectormul(vector&A,LL b)
{
    LL t=0;
    vectorC;
    for(int i=0;i<A.size()||t;i++)
    {
        if(i1&&!C.back())C.pop_back();
    return C;
}
void divide(LL x)
{
    for(int i=0;p[i]1)primes[x]+=2;
}
vectorres;
int main()
{
    res.push_back(1);
    scanf("%lld",&n);
    st[0]=st[1]=1;
    for(LL i=2;ibase)
            {
                res=mul(res,M);
                M=1;
            }
            M*=(primes[i]+1);
        }
    }
    if(M>1)res=mul(res,M);
    printf("%d",res.back());
    for(int i=res.size()-2;~i;i--)printf("%09d",res[i]);
    return 0;
}

[B]

原题

什么！是DP！

放TM的P,这简直是危言耸听

首先我们可以高高兴兴写出以下的代码 :

(取模、边界、循环省略)

if(j)
{
    f[i+1][j]+=f[i][j];
    f[i+1][j-1]+=f[i][j];
}
if(n-j)
{
    f[i+1][j]+=f[i][j];
    f[i+1][j+1]+=f[i][j];
}

然后会发现这个代码在自测样例2是过不了的。

为什么呢？

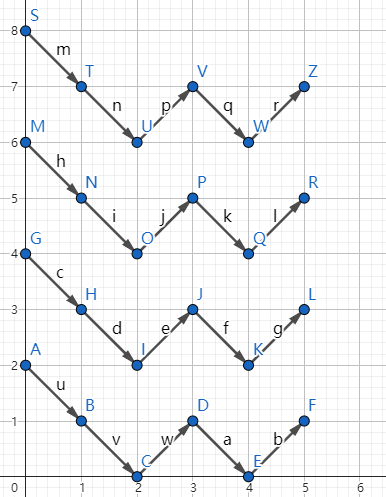
很显然这几条线段生成的序列是一样的。

考虑去重的问题。

很显然我们并没有办法精确且快速描述图像形状，因此考虑我们就指定其中一个有效。

我们考虑只有经过坐标轴的序列有效，其余无效，这样就可以不重不漏统计了。

CODE:

#include
using namespace std;
const int N=3e3+5;
typedef long long LL;
int n,m,mod;
LL f[N][N][2];
int main()
{
    freopen("easyhard.in","r",stdin);
    freopen("easyhard.out","w",stdout);
    scanf("%d%d%d",&n,&m,&mod);
    for(int i=1;i<=n;i++)f[0][i][0]=1;
    f[0][0][1]=1;
    for(int i=0;i<m;i++)
    {
        for(int j=0;j<=n;j++)
        {
            if(j)
            {
                if(j==1)
                {
                    f[i+1][j][1]=((f[i+1][j][1]+f[i][j][0])%mod+f[i][j][1])%mod;
                    f[i+1][j-1][1]=((f[i+1][j-1][1]+f[i][j][0])%mod+f[i][j][1])%mod;
                }
                else
                {
                    f[i+1][j][0]=(f[i+1][j][0]+f[i][j][0])%mod;
                    f[i+1][j][1]=(f[i+1][j][1]+f[i][j][1])%mod;
                    f[i+1][j-1][0]=(f[i+1][j-1][0]+f[i][j][0])%mod;
                    f[i+1][j-1][1]=(f[i+1][j-1][1]+f[i][j][1])%mod;
                }
            }
            if(n-j)
            {
                f[i+1][j][0]=(f[i+1][j][0]+f[i][j][0])%mod;
                f[i+1][j][1]=(f[i+1][j][1]+f[i][j][1])%mod;
                f[i+1][j+1][0]=(f[i+1][j+1][0]+f[i][j][0])%mod;
                f[i+1][j+1][1]=(f[i+1][j+1][1]+f[i][j][1])%mod;
            }
        }
    }
    LL res=0;
    for(int i=0;i<=n;i++)res=(res+f[m][i][1])%mod;
    printf("%lld",res);
    return 0;
}
训练日志

发表回复