聚龙DAY6

1.图论

（其实我OJ的图论专题还没打完

1.floyd

3重循环，枚举中转点
（但k(中转点)的循环要写外面

for(int k=1;k<=n;k++)
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(a[i][k]+a[k][j]<a[i][j])
            {
                a[i][j]=a[i][k]+a[k][j];
                path[i][j]=path[k][j];//记录路径
            }
        }
    }
}

2.dijkstra

非常简单
就是对不会堆的孩子来说，堆优化是什么东西？
小根堆：
priority_queue<int,vector，greater>//小根堆
（qjk讲的如何实现小根堆：
首先定义一个大根堆，然后push(-x),输出再×-1就好了
（非常的神奇，但没毛病

dijkstra+堆优化代码实现：

#include
using namespace std;
#define int long long 
#define rep(i,l,n) for(int i=l;i<=n;i++)
typedef pair pai;
const int N=1005,M=10005;
int h[N],e[M],ne[M],w[M],idx,dist[N];
bool f[N];
int n,m;
void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}//邻接表存储图 
int dijkstra()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    priority_queue<pai,vector,greater> q;//小根堆
    q.push({0,1});
    while(q.size())
    {
        auto t=q.top();
        q.pop();
        int two=t.second;
        if(f[two]) continue;
        f[two]=true;
        for(int i=h[two];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[two]+w[i])
            {
                dist[j]=dist[two]+w[i];
                q.push({dist[j],j});
            }
        }
    }
    if(dist[n]==0x3f3f3f3f) return -1;
    return dist[n];
}
signed main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    rep(i,1,m)
    {
        int u,v,w;
        cin>>u>>v>>w;
        add(u,v,w);
    }
    cout<<dijkstra()<<endl;
    return 0;
}

//注：此代码也是J组最后一题的代码
//无优化的以前打过了，在OJ里，懒的翻了
朴素版（无优化，代码如下：

void dijkstra(int xi) {
    for(int i=1;i<=n;i++) dis[i]=g[xi][i];
    dis[xi]=1;
    f[xi]=1;//记录状态
    for(int i=1;i<n;i++) 
    {
        maxn=0;
        for(int j=1;jmaxn) 
            {
                k=j;
                maxn=dis[j];
            }
        }
        f[k]=1; 
        if(k==y) break;
        for(int j=1;jdis[j]) 
                dis[j]=dis[k]*g[k][j];
        }       
    }
}

3.Bellman-Ford

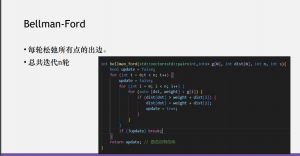
4.SPFA

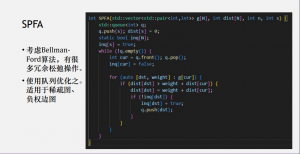
5.Prim

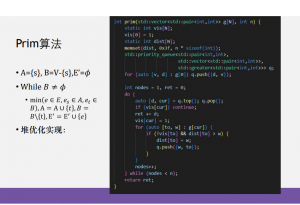
6.Kruskal

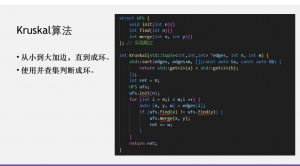
7.查分约束系统

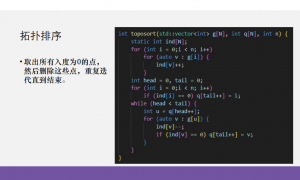
8.拓扑排序

2.比赛

S组：10/400 J组100/400
S组炸了，第一次简单但是没想到，（更没想到后面暴力炸了
J组：剩下没看，打了最后一题
一眼图最短路径，是今天讲的，so我打了
（原来一直输出-1，发现时if中的少了一个
我用的dijkstra+堆优化（代码见上
但是dijkstra 应该也可以过，毕竟数据小的可怜
上面除了floyd的算法应该都可以过,但是我喜欢堆优化
寒假教过图论，所以今天是唯一听全懂的一天