今天只讲点分治

用处：nlogn枚举树上所有路径

思路：

把路径分为有经过一个点的和没经过的

有经过的很简单，以这个点为根遍历就行了

没经过的路径就是把这个点删掉，剩下裂开的子树跑一遍上述操作

那怎么找这个点使复杂度最优呢？？

跟分治一个思路，尝试让每一次删点，裂开的子树缩小X倍

这样每个点最多遍历到logn次，就能达到nlogn复杂度

定义这个点为重心：一个以它为根节点，子树最大值最小的点；

经典最大值最小，可以让这个点处在相对“中间”的位置

如图

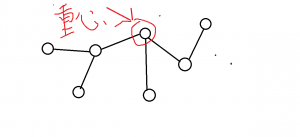
割完后：

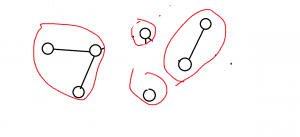
直接裂成很多小子树；

接下来再在子树上跑就行了

模板代码：

void find(int x,int fa)//找重心
{
    sz[x]=1;
    long long now=0; 
    for(int i=0;i<q[x].size();i++)
    {
        int y=q[x][i].v;
        if(y!=fa&&vis[y]==0)
        {
            find(y,x);
            sz[x]+=sz[y];
            now=max(now,sz[y]);
        }
    }
    now=max(now,all-sz[x]);
    if(now<ms) 
    {
        ms=now;
        rt=x;
    }
}
void getdis(int x,int cnt,int fa)//算子树内容（因题而异）
{
    sz[x]=1;
    for(int i=0;i<q[x].size();i++)
    {
        int y=q[x][i].v;
        if(y!=fa&&vis[y]==0)
        {
            top++;
            a[top]=cnt+q[x][i].w;
            getdis(y,cnt+q[x][i].w,x);
            sz[x]+=sz[y];
        }
    }
}
int cl(int x,int cnt)//计算答案（因题而异）
{
    int sum=0;
    top=1;
    a[top]=cnt;
    getdis(x,cnt,0);
    sort(a+1,a+top+1);
    for(int i=1,j=top;i<=top&&j>i;i++)
    {
        while(a[i]+a[j]>k&&j>i) j--;
        sum+=j-i;
    }
    return sum;
}
void dfs(int x)//遍历所有点
{
    vis[x]=1;
    ans+=cl(x,0);
    for(int i=0;i<q[x].size();i++)
    {
        int y=q[x][i].v;
        if(vis[y]==0)
        {
            ans-=cl(y,q[x][i].w);
            ms=1145141919;
            all=sz[y];
            find(y,x);
            dfs(rt);
        }
    }
}
//四个主要函数