- 今天虽然是这次集训的最后一天,但是想到集训后又得去上补习班,悲从中来
- sob: :sob: :sob: :sob: :sob:
上午比赛
怎么说呢,130一般般,最后一题知道是并查集,但是考试时忘记如何查询元素个数了:sweat:,考完才发现T2之前做过
下午:拓扑排序+关键路径
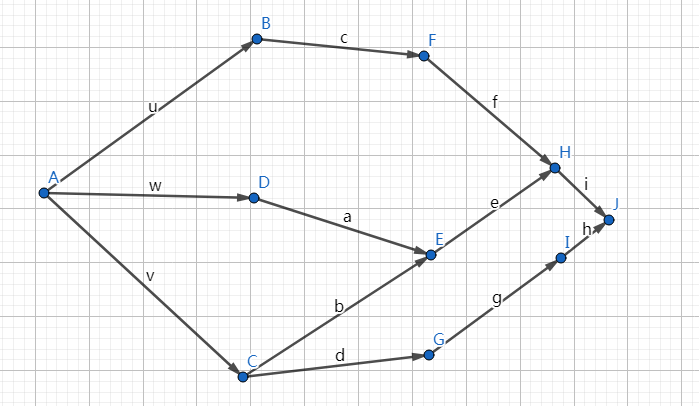
如何求拓扑序列?
如图
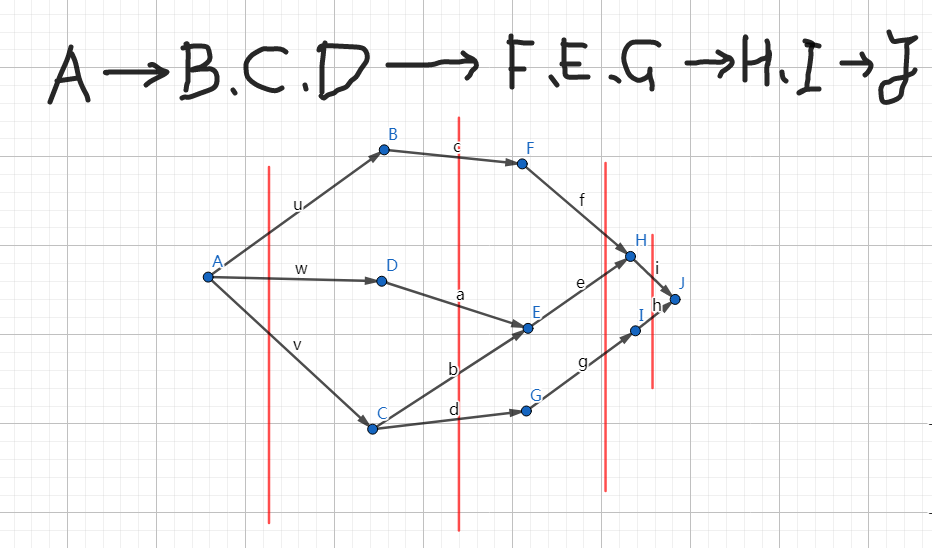
不难发现,拓扑序列实际上是通过将图分层后遍历每层所得到的序列
这不禁能够联想到BFS
所以实际上我们完全可以通过BFS得到一个图的拓扑序列,代码如下:
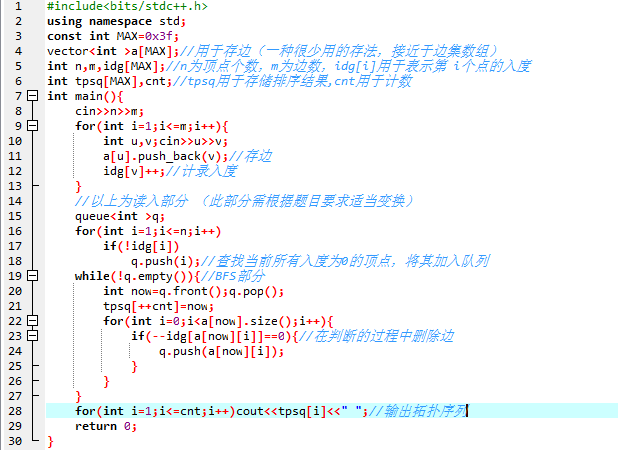
关键路径
当一个有向图中不存在环且存在唯一的入度为0的点与唯一的出度为0的点时,才会存在关键路径
仍如图
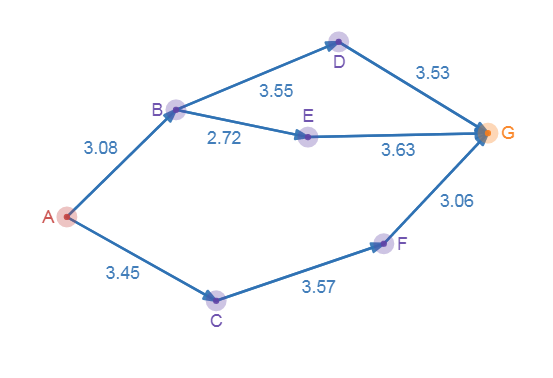
我们假定顶点表示事件,边是活动,边权为花费的时间
引理1:关键路径必然包含入度或出度为0的点,并以入度为零的点作为源点,出度为0的点为终点
引理2:在关键路径内的点,其事件最早发生时间与最晚发生时间间隔为0
所以,由此我们可以推出我们可以利用拓扑排序进行对每个事件的最早开始时间进行记录
令etime表示事件发生的最早时间,ltime是事件发生的最晚事件
有公式etime[i]=max(etime[j]+w[i][j],etime[i]),其中我们令etime[1]=1
再利用逆拓扑排序求出每个活动的最晚开始时间
有公式ltime[i]=min(ltime[j]-w[j][i],ltime[i]),其中我们令ltime[n]=etime[n]
最后再用两数组相减,查看其值是否为0即可,代码略(其实逆拓扑排序只需在原算法的基础上,将图反向即可)
有时若要求活动的最早或最晚开始时间,假定编号为x的边是Edge,有公式:
aetime[x]=etime[u]
altime[x]=ltime[v]-w[u][v]
此处aetime与altime类比etime与ltime
整活
有好东西
好东西