Winter Vacation Training Day 4 (01.30)

Extend 4.1 : Topological Sort

Example :

Figure 9.1 : Topological Sort

Topological Sort is an algorithm to solve the under sequence in DAG(Directed Acyclic Graph) :

DAG is a directed graph that there is no cycle in the graph.

If the sequence is T, and there is an edge (A, B),
The index of A in T is before B.

For the algorithm, we need to know the indegree of all nodes.

Indegree of A : ||I|| ((I, A) are all in E.)

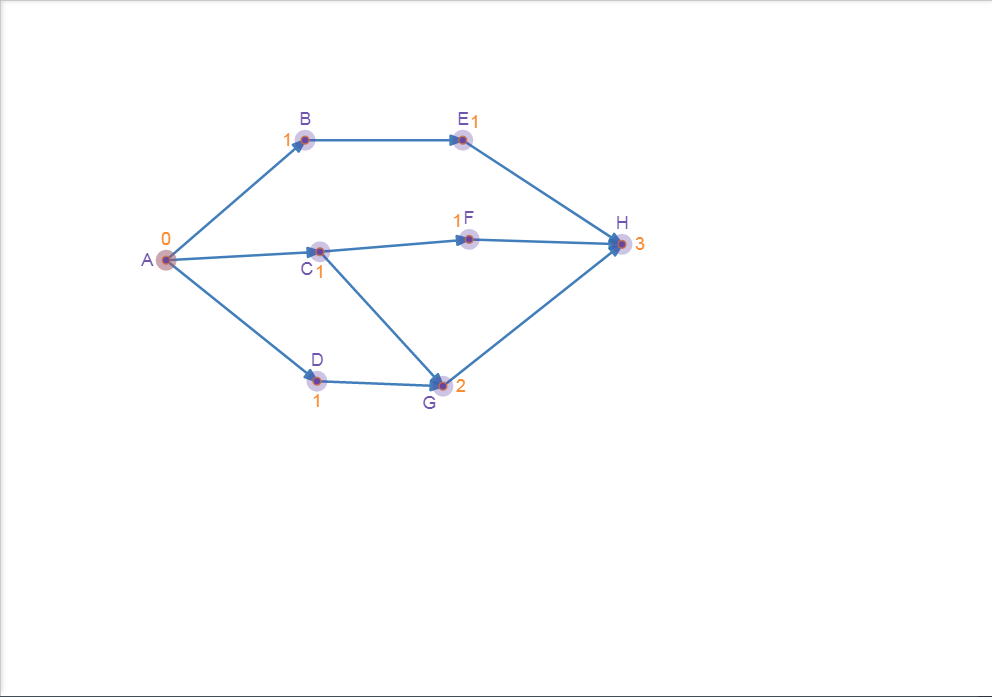
Figure 9.2 : Indegree

Step 1, find the node with indegree 0 (here is A). Then, delete the node and all related edges.

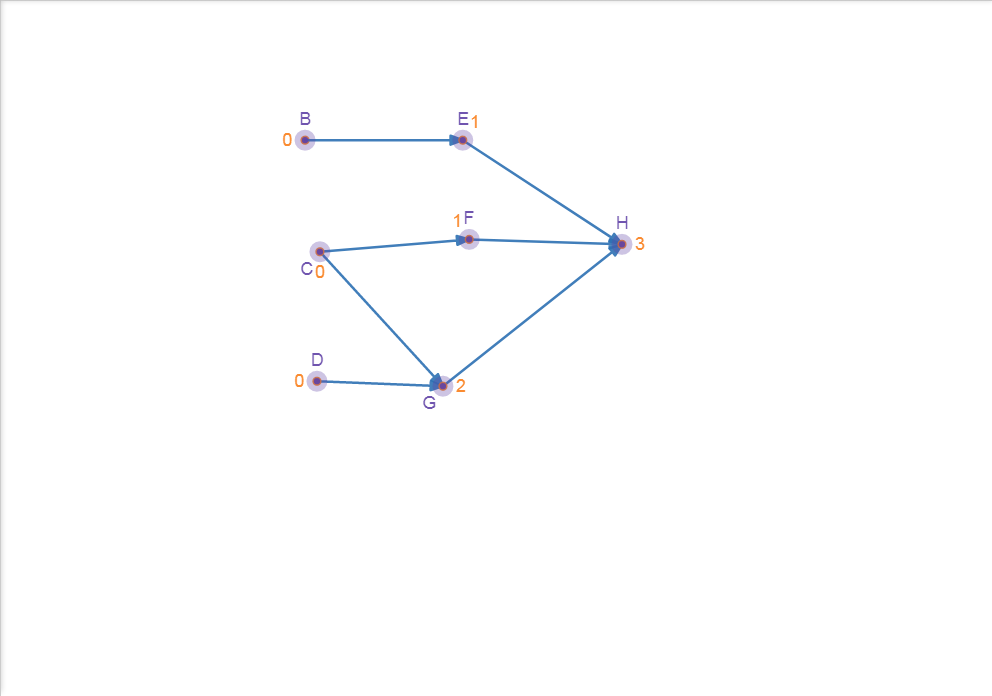
Figure 9.3-a : Topological Sort(a)

(T = [A])

Now, we get 3 nodes with indegree 0. Do as that again.

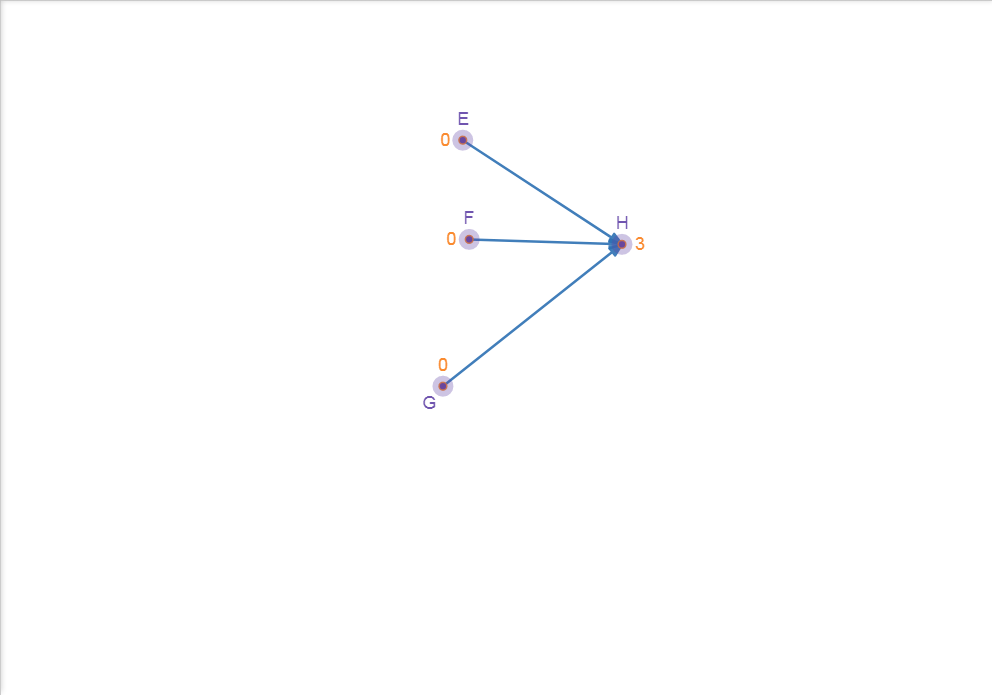
Figure 9.3-b: Topological Sort(b)

(T = [A, B, C, D])

And again and again…

Figure 9.3-c : Topological Sort(c)

(T = [A, B, C, D, E, F, G])

Now we get the topological sequence T of the DAG.

We can also proof the graph with cycle hasn’t T.

proof

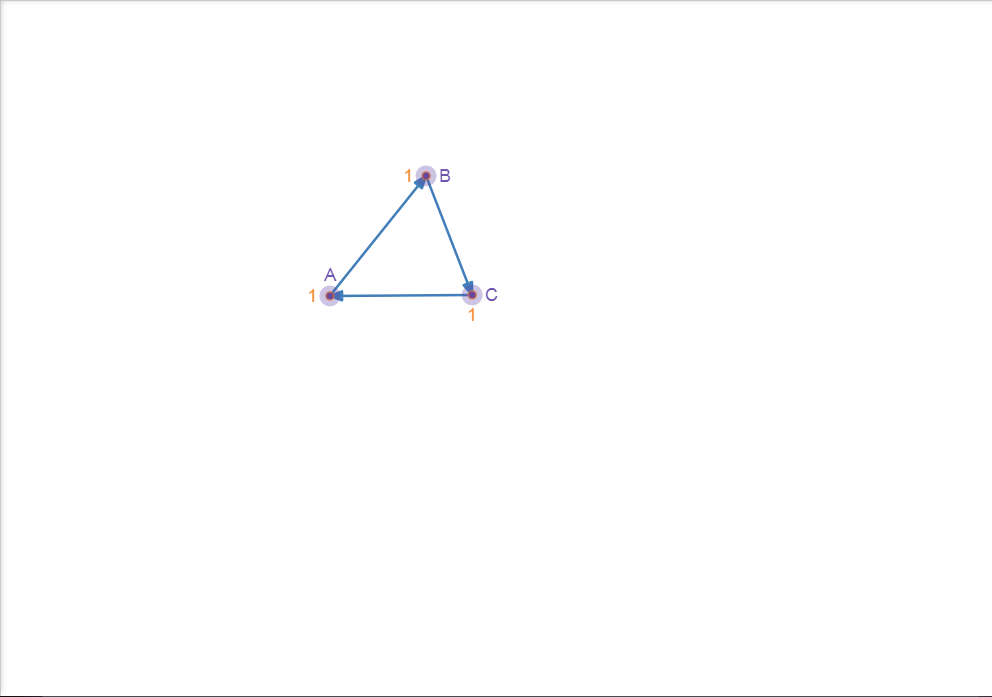
Figure 9.4 : Graph with cycle
As Figure 9.4, all indegrees of nodes are all not 0, so we can’t add any nodes to T.
So, the graph has no T.

This is Topological Sort.

Given Score :
    Difficulty : 1
x   Basic Score : 61
Score : 899
[Area 3.1 Unlocked]