今天早上打套题，简单的来解析一下

T1迷宫问题

题目如下图：

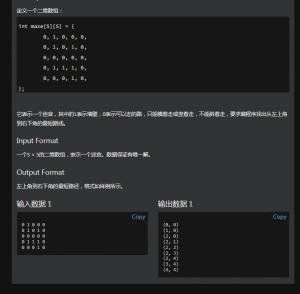
不难发现这是一个用搜索就能AC的题目（广搜完全可以，深搜因为才5*5的矩形所以也够用），但考试上没注意输出中间用空格，因此惨痛爆零

T2家庭问题

题目：

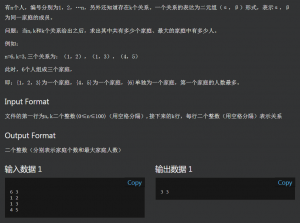
这一题之前在栈还是队列中打过，记忆犹新，说是要用并查集但用搜索依旧AC

T3路面加宽问题

题目：

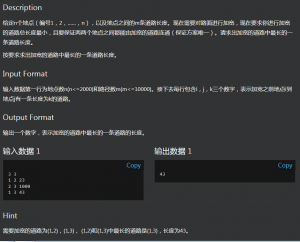
这一题为最小生成树问题，但早上不会，实际上它就是个模板题

T4单行道

题目：

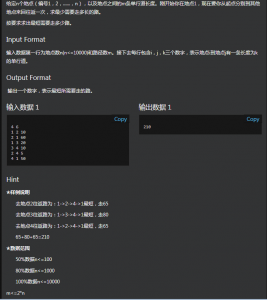
“Dijkstra”（用“floyd”过不了，zmx以分数换来的教训），但算回路是要想着倒过来求

---

接下来是算法部分，今天讲了并查集和最小生成树

并查集

并查集的重要思想在于，用集合中的一个元素代表集合。我曾看过一个有趣的比喻，把集合比喻成family，而代表元素则是father，其他元素就是子孙
把并查集三个字拆开即可得到合并，查询，以及集合。So我们可以写出最简单版本的并查集代码

//初始化
int fa[MAXN];
inline void init(int n)
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
}
//假如有编号为1, 2, 3, ..., n的n个元素，我们用一个数组fa[]来存储每个元素的父节点（因为每个元素有且只有一个父节点，所以这是可行的）。一开始，我们先将它们的父节点设为自己。

//查询
int find(int x)
{
    if(fa[x] == x)
        return x;
    else
        return find(fa[x]);
}
//我们用递归的写法实现对代表元素的查询：一层一层访问父节点，直至根节点（根节点的标志就是父节点是本身）。要判断两个元素是否属于同一个集合，只需要看它们的根节点是否相同即可。

//合并
inline void merge(int i, int j)
{
    fa[find(i)] = find(j);
}
//合并操作也是很简单的，先找到两个集合的代表元素，然后将前者的父节点设为后者即可。当然也可以将后者的父节点设为前者，这里暂时不重要。本文末尾会给出一个更合理的比较方法。

最简单的并查集效率是比较低的,因此我们可以使用路径压缩的方法。既然我们只关心一个元素对应的根节点，那我们希望每个元素到根节点的路径尽可能短，最好只需要一步。合并（路径压缩）
其实这说来也很好实现。只要我们在查询的过程中，把沿途的每个节点的父节点都设为根节点即可。下一次再查询时，我们就可以省很多事。

//合并（路径压缩）
int find(int x)
{
    if(x == fa[x])
        return x;
    else{
        fa[x] = find(fa[x]);  //父节点设为根节点
        return fa[x];         //返回父节点
    }
}

//也可以
int find(int x)
{
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}

路径压缩优化后，并查集的时间复杂度已经比较低了，绝大多数不相交集合的合并查询问题都能够解决。然而，对于某些时间卡得很紧的题目，我们还可以进一步优化.
我们用一个数组rank[]记录每个根节点对应的树的深度（如果不是根节点，其rank相当于以它作为根节点的子树的深度）。一开始，把所有元素的rank（秩）设为1。合并时比较两个根节点，把rank较小者往较大者上合并。
路径压缩和按秩合并如果一起使用，时间复杂度接近O(n)
，但是很可能会破坏rank的准确性。

//初始化（按秩合并）
inline void init(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        fa[i] = i;
        rank[i] = 1;
    }
}

//合并（按秩合并）
inline void merge(int i, int j)
{
    int x = find(i), y = find(j);    //先找到两个根节点
    if (rank[x] <= rank[y])
        fa[x] = y;
    else
        fa[y] = x;
    if (rank[x]  rank[y] && x != y)
        rank[y]++;                   //如果深度相同且根节点不同，则新的根节点的深度+1
}

最小生成树

概念：图上有n个点，我们要用n-1或n条边去连接他们
最小生成树有两个归并方向，一个是边+权，另一个是点+权！所以我们去求最小生成树就有两种方法—Kruskal（边）和Prim算法（点）
Prim–点
此算法可以称为“加点法”，每次遍历选择代价最小的边对应的点，加入到最小生成树数组中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。是不是感觉他与Dijkstra算法思路有相似之处？
图的所有顶点集合为g；初始令集合u={A},v=g−u;在两个集合u,v能够组成的边中，选择一条代价最小的边(u0,v0)，加入到最小生成树中，并把v0并入到集合u中。重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。由于不断向集合u中加点，所以最小代价边必须同步更新；需要建立一个辅助数组st,用来维护集合v中每个顶点与集合u中最小代价边信息：
简单来说就是我们线初始化一个dist数组，然后我们去遍历他！找到一个集合外最近的点t，然后再用t去更新其他点到集合的距离，然后改变他的状态！

---

Kruskal——边
此算法可以称为“加边法”，初始最小生成树边数为0，每遍历一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。对于图我们不一定要用邻近表来存储或其他的数据结构，用结构体就好了！！

1. 把图中的所有边按权重从小到大排序（STL快乐）；
2. 把图中的n个顶点看成独立的n棵树组成的森林；
3. 按权值从小到大枚举边，所选的边连接的两个顶点ui,vi如果不连通，则将它们成为最小生成树集合的一条边（并查集的思想），并将这两颗树合并作为一颗树。）
4. 重复(3),直到所有顶点都在一颗树内或者有n-1条边为止。

---

今天依旧充实，心情依旧美好（也许是因为期末考两校区第九的成绩吧，边上的zmx羡慕死了），明天加油