Winter Vacation Training Day 3 (01.29)

Area 3.1 : Kruskal

Example :

Figure 7.1 : Kruskal
Kruskal is an algorithm solving MST(mininum spanning tree).

Spanning Tree(V’, E’) : V’ == V, E’ is in E and ||E’|| = ||V|| – 1
(It is a tree with edges in the graph and all nodes of the graph.)

We didn’t need anything, except edges.

Step 1, find the edge with mininum weight (and won’t build a cycle)(Here is (1, 3) = 4.59) and add it to ST.

Figure 7.2-a : Kruskal(a)

(Orange edges and nodes are in ST.)

Then find the mininum edge in remain edges (and won’t build a cycle)(Here is (2, 6) = 5.2) add it to ST.

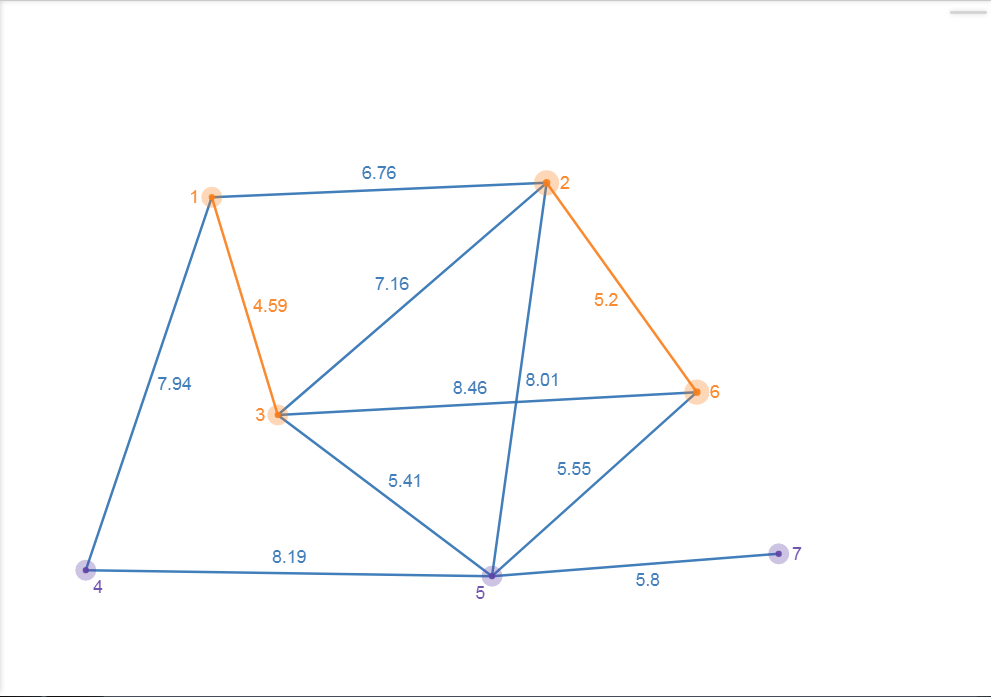
Figure 7.2-b : Kruskal(b)

Repeat again

Figure 7.2-c : Kruskal(c)

Next one is (5, 6) = 5.55. Even 5 and 6 are both in ST, if there is not a cycle, we can still add the edges to ST.

Figure 7.2-d : Kruskal(d)

Again

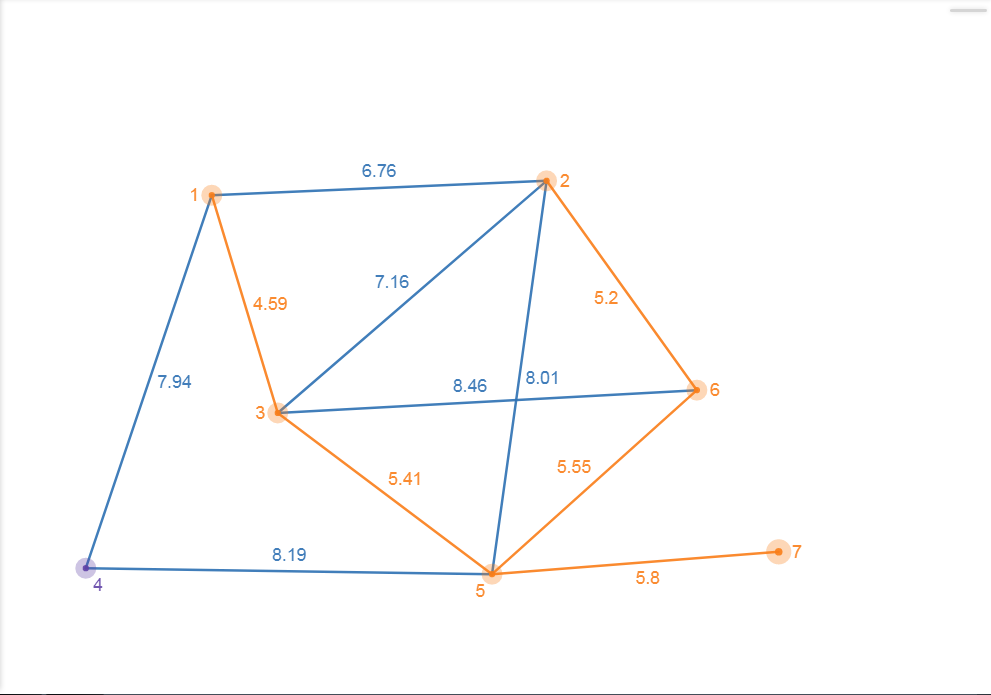
Figure 7.2-e : Kruskal(e)

Next is (1, 2) = 6.76. But if we add this edge, there will be a cycle 1-2-6-5-3.So we skip it.

Here’s the result.

Figure 7.2-f : Kruskal(f)

The weight of MST is 34.49.

This is Kruskal.

Given Score :
    Difficulty : 2
x   Basic Score : 126
Score : 750