长乐寄训DAY2

Posted on By 吴, 吴玮航

看到这句奇怪的话了吗？
等我有空写一篇Blog来介绍吧
———————————

前排提示：不要相信cjx的话

另外，挂一个大佬
上午
这是题目
T1 看到对于10%的数据，n=1,直接判断奇偶输出1或2，拿完10分走人

T2 同上，对于10%的数据，W i=1,对于另外20%的数据，n<=2,所以简单粗暴地用max（）,min()大法暴力地模拟每一种情况，代码如下（硬水）

#include
using namespace std;
int n,w[10],h[10],v,ans,a[10],b[10];
int main()
{
    freopen("rectangle.in","r",stdin);
    freopen("rectangle.out","w",stdout);
    cin>>n;
    for(int i=1;i>w[i]>>h[i];
        a[i]=w[i];
        b[i]=h[i];
        if(w[i]!=1)
        {
            v=1;
        }
        ans+=h[i];
    }
    if(v==0)
    {
        cout<<ans<<endl;
        return 0;
    }
    else
    {
        ans=2147483647;
    }
    if(n==1)
    {
        cout<<w[1]*h[1]<<endl;
        return 0;
    }
    if(n==2)
    {
        ans=min(ans,(w[1]+w[2])*max(h[1],h[2]));
        ans=min(ans,(w[1]+h[2])*max(w[2],h[1]));
        ans=min(ans,(w[2]+h[1])*max(w[1],h[2]));
        ans=min(ans,(h[1]+h[2])*max(w[1],w[2]));
        cout<<ans<<endl;
        return 0;
    }
    if(n==3)
    {
        for(int i=1;i<=3;i++)
        {
            w[i]=a[i];
            h[i]=b[i];
        }
        w[2]+=w[3];
        h[2]=max(h[2],h[3]);
        ans=min(ans,(w[1]+w[2])*max(h[1],h[2]));
        ans=min(ans,(w[1]+h[2])*max(w[2],h[1]));
        ans=min(ans,(w[2]+h[1])*max(w[1],h[2]));
        ans=min(ans,(h[1]+h[2])*max(w[1],w[2]));
        for(int i=1;i<=3;i++)
        {
            w[i]=a[i];
            h[i]=b[i];
        }
        w[2]+=h[3];
        h[2]=max(h[2],w[3]);
        ans=min(ans,(w[1]+w[2])*max(h[1],h[2]));
        ans=min(ans,(w[1]+h[2])*max(w[2],h[1]));
        ans=min(ans,(w[2]+h[1])*max(w[1],h[2]));
        ans=min(ans,(h[1]+h[2])*max(w[1],w[2]));
        for(int i=1;i<=3;i++)
        {
            w[i]=a[i];
            h[i]=b[i];
        }
        w[1]+=w[3];
        h[1]=max(h[1],h[3]);
        ans=min(ans,(w[1]+w[2])*max(h[1],h[2]));
        ans=min(ans,(w[1]+h[2])*max(w[2],h[1]));
        ans=min(ans,(w[2]+h[1])*max(w[1],h[2]));
        ans=min(ans,(h[1]+h[2])*max(w[1],w[2]));
        for(int i=1;i<=3;i++)
        {
            w[i]=a[i];
            h[i]=b[i];
        }
        w[1]+=h[3];
        h[1]=max(h[1],w[3]);
        ans=min(ans,(w[1]+w[2])*max(h[1],h[2]));
        ans=min(ans,(w[1]+h[2])*max(w[2],h[1]));
        ans=min(ans,(w[2]+h[1])*max(w[1],h[2]));
        ans=min(ans,(h[1]+h[2])*max(w[1],w[2]));
        cout<<ans<=4)
    {
        cout<<"?"<<endl;
    }
}

T3 依然是暴力地收拾掉30%的数据，直接循环+数字拆分，没什么好说的,代码也就不贴了

下午
T1 看到标红的这行没，比赛时少打了这一行，原来70分的代码直接爆零了

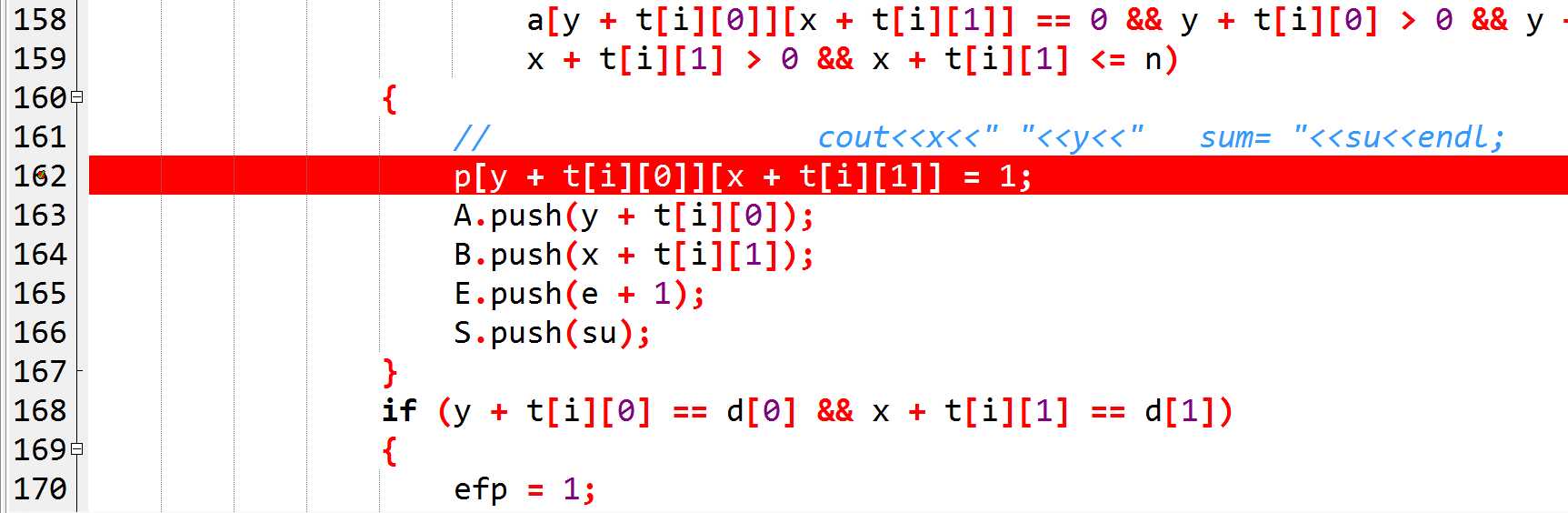
啊没错，就是bfs的时候忘记了标记走过的路径，然后要么TLE要么MLE（这玩意是怎么过的样例的啊）简单来说下这题吧。这是题目链接。首先这题要用到二分，不然还是会TLE。首先对每个H进行一遍BFS，求出每个单位时间的障碍的位置分布，但为了不超时将这些BFS合并成一遍，用数字表示在某个单位时间出现的障碍（详见代码就是懒），然后在二分里面进行路径的BFS，并在BFS中根据单位时间来判断障碍，大概就是这样
代码如下

#include 
using namespace std;
int n, k, a[805][805], m[2], d[2], v[805][805], sum, anstrue;
int x, y, e, t[4][2] = { 1, 0, 0, 1, -1, 0, 0, -1 };
string ss;
int l, r, mi, efp, su;
bool p[805][805];
queue A;
queue B;
queue E;
queue S;
int main()
{
    freopen("mecho.in", "r", stdin);
    freopen("mecho.out", "w", stdout);
    cin >> n >> k;
    for (int i = 1; i > ss;
        for (int j = 1; j <= n; j++)
        {
            if (ss[j - 1] == &#039;T&#039;)
            {
                a[i][j] = 1;
            }
            if (ss[j - 1] == &#039;H&#039;)
            {
                a[i][j] = 2;
            }
            if (ss[j - 1] == &#039;M&#039;)
            {
                a[i][j] = 3;
                m[0] = i;
                m[1] = j;
            }
            if (ss[j - 1] == &#039;D&#039;)
            {
                a[i][j] = 4;
                d[0] = i;
                d[1] = j;
            }
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            v[i][j] = 2147483647;
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            if (a[i][j] == 2)
            {
                A.push(i);
                B.push(j);
                E.push(1);
                v[i][j] = 0;
            }
        }
    }
    while (!A.empty())
    {
        x = B.front();
        y = A.front();
        e = E.front();
        A.pop();
        B.pop();
        E.pop();
        for (int k = 0; k  e && y + t[k][0] > 0 &&
                    y + t[k][0]  0 && x + t[k][1] <= n)
            {
                //                          cout<<e<<" "<<x<<" "<<y<<endl;
                v[y + t[k][0]][x + t[k][1]] = e;
                A.push(y + t[k][0]);
                B.push(x + t[k][1]);
                E.push(e + 1);
            }
        }
        //                  cout<<"Dd"<<endl;
    }

<pre><code>/*  cout<<endl;
        for(int i=1;i<=n;i++)
        {
                for(int j=1;j<=n;j++)
                {
                        if(a[i][j]==1)
                        {
                                cout<<"T";
                        }
                        else
                        {
                                if(v[i][j]==2147483647)
                                {
                                        cout<<"O";
                                }
                                else
                                  cout<<v[i][j];
                        }
                }
                cout<<endl;
        }*/

for (int i = 1; i <= n; i++)
{
    for (int j = 1; j <= n; j++)
    {
        if (v[i][j] != 2147483647)
        {
            r = max(r, v[i][j]);
        }
    }
}
//  cout<<r< l + 1)
{
    //      cout<<l<<" "<<r<<endl;
    mi = (l + r) / 2;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= n; j++)
        {
            p[i][j] = 0;
        }
    }
    A.push(m[0]);
    B.push(m[1]);
    p[m[0]][m[1]] = 1;
    E.push(0);
    sum = -1;
    sum += mi;
    S.push(sum);
    efp = 0;
    while (!A.empty())
    {
        //          cout<<" xy  "<<x<<" "<<y<<endl;
        x = B.front();
        y = A.front();
        e = E.front();
        su = S.front();
        A.pop();
        B.pop();
        E.pop();
        S.pop();
        if (e % k == 0)
        {
            su++;
        }
        for (int i = 1; i  su || v[y + t[i][0]][x + t[i][1]] == 2147483647) &&
                    a[y + t[i][0]][x + t[i][1]] == 0 && y + t[i][0] > 0 && y + t[i][0]  0 && x + t[i][1] <= n)
            {
                //                  cout<<x<<" "<<y<<"   sum= "<<su<<endl;
                p[y + t[i][0]][x + t[i][1]] = 1;
                A.push(y + t[i][0]);
                B.push(x + t[i][1]);
                E.push(e + 1);
                S.push(su);
            }
            if (y + t[i][0] == d[0] && x + t[i][1] == d[1])
            {
                efp = 1;
                //                  cout<<mi<<" OK"<<endl;
                while (!A.empty())
                {
                    A.pop();
                    B.pop();
                    E.pop();
                    S.pop();
                }
            }
        }
    }
    if (efp == 1)
    {
        l = mi;
        anstrue = 1;
    }
    else
    {
        r = mi;
    }
    //      cout<<"test   "<<l<<" "<<r<<" "<<mi<<endl;
}
if (anstrue == 1)
    cout << l << endl;
else
    cout << "-1" << endl;
</code></pre>

}
训练日志