T1

原题链接
请注意原题中卡空间会比较严。
是一个DP，但是考试的时候打挂了。
定义f[l][r][w]为在l~r的区间中，当前的人选取的C的个数。
然后记忆化搜索。
可以参考代码，式子长这样：
f[l][r][w]=0(w>=k)
f[l][r][w]=1(v>=k)
f[l][r][w]=!f[l+1][r][v]|!f[l][r-1][v](其他情况)

#include<bits/stdc++.h>
using namespace std;
const int N=355;
int k,n,f[N][N][N];
char str[N];
int dfs(int l,int r,int a,int b)
{
    if(!a)return -1;
    if(!b)return 1;
    if((n-(r-l))%2&&f[l][r][a])return f[l][r][a];
    if((!((n-(r-l))%2))&&f[l][r][b])return f[l][r][b];
    if((n-(r-l))%2)
    {
        if(~dfs(l+1,r,a-(str[l]=='C'),b)||~dfs(l,r-1,a-(str[r]=='C'),b))return f[l][r][a]=1;
        else return f[l][r][a]=-1;
    }
    else
    {
        if(~dfs(l+1,r,a,b-(str[l]=='C'))&&~dfs(l,r-1,a,b-(str[r]=='C')))return f[l][r][b]=1;
        return f[l][r][b]=-1;
    }
}
int main()
{
    scanf("%d%d%s",&n,&k,str+1);
    if(~dfs(1,n,k,k))puts("DA");
    else puts("NE");
    return 0;
}

T2

原题链接
请注意本题中模数可改变（且需要一些求逆元优化）。
对于这个式子，我们将d提出来，
特判d=0，答案为a^n
然后答案为：

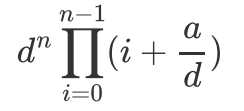
预处理逆元/阶乘就可以了。

T3

注意到我们要求对于所有点为出发点的答案。而能使A胜利的点集S将会随着终点T变小而越来越大。所以我们从大到小枚举终点T，同时维护S，这样就可以直接算出所有答案。
这样使用BFS去做，是O(n+m)的。