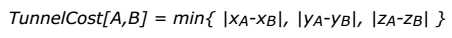T1
有n个大人和m个小孩将要去乘大巴。已知小孩是不能自己乘坐做的,必须有大人带着。每个大人可以带多个孩子,但是只有其中的一个孩子是不用买票的,其余他带着的小孩都要买票。由于不知道大人和小孩之间的关系,请你算算最多和最少需要买多少张票?
分类讨论。
#include <bits/stdc++.h>
using namespace std;
int n, m;
int main() {
scanf("%d%d", &n, &m);
if (!n && !m) {
puts("0 0");
return 0;
}
if (!n) {
puts("Impossible");
return 0;
}
if (!m) {
printf("%d %d", n, n);
return 0;
}
printf("%d %d\n", n + max(0, m - n), n + m - 1);
return 0;
}
T2
Tai_zong和朋友们分好组去郊游,他们只想乘出租车。每一组分别有s[i]个人(1<=s[i] 已知有N个区间,每个区间的范围是[Si,Ti],请求出区间覆盖后的总长。
是一个基础的算法,在这里
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
int n;
LL res;
vector<pair<LL, LL> > V, ans;
#define x first
#define y second
int main() {
scanf("%d", &n);
while (n--) {
LL a, b;
scanf("%lld%lld", &a, &b);
V.push_back({ a, b });
}
sort(V.begin(), V.end());
LL st = -1, ed = -1;
for (int i = 0; i < V.size(); i++) {
if (ed < V[i].first) {
if (~st && ~ed)
ans.push_back({ st, ed });
st = V[i].x;
ed = V[i].y;
}
ed = max(ed, V[i].y);
}
ans.push_back({ st, ed });
for (int i = 0; i < ans.size(); i++) res += (ans[i].y - ans[i].x + 1);
printf("%lld\n", res);
return 0;
}
T4
邪恶的生物学家找到了一段奇怪的基因片段,是由“A”,“B”组成的。他想做一个实验,前提是把所有基因片段中的“B”变成“A”,让整段基因只由“A”组成。作为他的助手,你的任务就是完成这个的实验的准备工作。现在给你两种酶,有以下功效:
每单位的酶S可以将基因片段中的单个“B”变成“A”,或将“A”变成“B”;
每单位的酶P可以将基因片段中的某一前缀翻转,“B”变成“A”,“A”变成“B”。
为了节约药品,请你算一算,你总共最少需要多少单位的酶来完成准备工作。
对于一个i来说,如果s[i]不等于s[i-1],则意味着s[i~n]均要翻转
但是有一种特殊情况,s[i-1]=s[i+1]时,只需要单独改变s[i]
#include <bits/stdc++.h>
using namespace std;
const int N = 1000005;
int n, res;
char s[N];
int main() {
scanf("%d%s", &n, s + 1);
for (int i = 2; i <= n; i++) {
if (s[i] != s[i - 1]) {
s[i] = s[i + 1];
res++;
}
}
res += (s[n] == 'B' ? 1 : 0);
printf("%d", res);
return 0;
}
T5
在小C统治宇宙之后(纯属YY),他决定建立一座时空隧道网络来连接不同的星球和星系。已知小C的宇宙共有N个星球,他们的坐标用3维(x,y,z)的形式给出,而任意两个星球之间建立时空隧道的代价为:
其中x,y,z分别表示星球的坐标。小C想建立N-1条时空隧道,刚好连接所有星球,并且需要建立隧道的花费尽可能小。作为他的总工程师,你能算出最小的代价么?
瞎猜一下结论(bushi。
对于x,y,z,分别进行排序,然后仅需连接相邻的两点。
边数成功由n^2 -> 3n
然后kruskal一下就可以了。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
typedef long long LL;
int n, cnt, st[N], par[N];
struct node {
int x, y, z;
};
int cmp(node a, node b) { return a.z < b.z; }
int find(int x) {
if (par[x] == x)
return x;
else
return par[x] = find(par[x]);
}
LL res = 0;
vector<pair<int, int> > X, Y, Z;
vector<node> G;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
par[i] = i;
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
X.push_back({ x, i });
Y.push_back({ y, i });
Z.push_back({ z, i });
}
sort(X.begin(), X.end());
sort(Y.begin(), Y.end());
sort(Z.begin(), Z.end());
for (int i = 1; i < X.size(); i++)
G.push_back({ X[i - 1].second, X[i].second, abs(X[i].first - X[i - 1].first) });
for (int i = 1; i < Y.size(); i++)
G.push_back({ Y[i - 1].second, Y[i].second, abs(Y[i].first - Y[i - 1].first) });
for (int i = 1; i < Z.size(); i++)
G.push_back({ Z[i - 1].second, Z[i].second, abs(Z[i].first - Z[i - 1].first) });
sort(G.begin(), G.end(), cmp);
for (int i = 0; i < G.size(); i++) {
int a = G[i].x, b = G[i].y, c = G[i].z;
a = find(a);
b = find(b);
if (a == b)
continue;
cnt++;
res += (LL)c;
par[a] = b;
if (cnt >= n - 1)
break;
}
printf("%lld", res);
return 0;
}
T6
吉哥这几天对队形比较感兴趣。
有一天,有n个人按顺序站在他的面前,他们的身高分别是h[1], h[2] … h[n],吉哥希望从中挑出一些人,让这些人形成一个新的队形,新的队形若满足以下三点要求,则称之为完美队形:
1、挑出的人保持他们在原队形的相对顺序不变;
2、左右对称,假设有m个人形成新的队形,则第1个人和第m个人身高相同,第2个人和第m-1个人身高相同,依此类推,当然,如果m是奇数,中间那个人可以任意;
3、从左到中间那个人,身高需保证递增,如果用H表示新队形的高度,则H[1] < H[2] < H[3] …. < H[mid]。
现在吉哥想知道:最多能选出多少人组成完美队形?
一眼DP,但是不会写,差点以为是合唱队形的原题。
然而不是,是一个LCIS。
有人当然说这题可以用manacher做,然而实际上manacher只能解决连续的回文问题。
这题的LCIS的a数组自然是原数组,b数组则是将a数组翻转得来的。
LCIS模板
#include <bits/stdc++.h>
using namespace std;
const int N = 5005;
int n, res, a[N], f[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int i = 1; i <= n; i++) {
int maxv = 0;
for (int j = n; j >= i; j--) {
if (a[i] == a[j])
f[j] = max(f[j], maxv + 1 + (i != j));
if (a[i] > a[j])
maxv = max(maxv, f[j]);
res = max(res, f[j]);
}
}
printf("%d", res);
return 0;
}
T7
LUOGU
最大流,二分。
先黑白染色,然后建立二分图。
判定时检验是否最大流流满。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int dx[4] = { -1, 0, 1, 0 };
const int dy[4] = { 0, -1, 0, 1 };
const int N = 10005, M = 200005;
const LL INF = 1e15;
int n, m, S, T;
int h[N], e[M], ne[M], idx;
LL f[M], w[45][45];
int d[N], q[N], cur[N];
void add(int a, int b, LL c) {
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++, e[idx] = a, f[idx] = 0, ne[idx] = h[b],
h[b] = idx++;
}
int get(int x, int y) { return (x - 1) * m + y; }
int bfs() {
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S;
d[S] = 0;
cur[S] = h[S];
while (hh <= tt) {
int u = q[hh++];
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (d[j] == -1 && f[i]) {
d[j] = d[u] + 1;
cur[j] = h[j];
if (j == T)
return 1;
q[++tt] = j;
}
}
}
return 0;
}
LL find(int u, LL limit) {
if (u == T)
return limit;
LL flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
cur[u] = i;
int j = e[i];
if (d[j] == d[u] + 1 && f[i]) {
LL t = find(j, min(f[i], limit - flow));
if (!t)
d[j] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
LL dinic() {
LL r = 0, flow;
while (bfs()) {
while (flow = find(S, INF)) r += flow;
}
return r;
}
int check(LL mid) {
memset(h, -1, sizeof h);
idx = 0;
LL sum = 0;
S = 0;
T = n * m + 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if ((i + j) & 1)
add(get(i, j), T, mid - w[i][j]);
else {
add(S, get(i, j), mid - w[i][j]);
sum += mid - w[i][j];
for (int k = 0; k < 4; k++) {
int nx = i + dx[k], ny = j + dy[k];
if (1 <= nx && nx <= n && 1 <= ny && ny <= m)
add(get(i, j), get(nx, ny), INF);
}
}
}
}
return dinic() == sum;
}
void work() {
scanf("%d%d", &n, &m);
LL Max = 0;
LL s1 = 0, s2 = 0, c1 = 0, c2 = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
scanf("%lld", &w[i][j]);
Max = max(Max, w[i][j]);
if ((i + j) & 1) {
s1 += w[i][j];
c1++;
} else {
s2 += w[i][j];
c2++;
}
}
}
if (c1 != c2) {
LL t = (s2 - s1) / (c2 - c1);
if (t >= Max && check(t))
printf("%lld\n", t * c1 - s1);
else
puts("-1");
} else {
if (s1 != s2)
puts("-1");
else {
LL l = Max, r = INF;
while (l < r) {
LL mid = l + r >> 1;
if (check(mid))
r = mid;
else
l = mid + 1;
}
if (l == INF)
puts("-1");
else
printf("%lld\n", l * c1 - s1);
}
}
}
int main() {
int T;
scanf("%d", &T);
while (T--) work();
return 0;
}