又寄了
T1 十年oi一场空,不开取模见祖宗。
总之本来是正解的解法(指1e7内能过,时间复杂度正确)因为没取模只有50分。又是和题解不一样的解法,但今天就不细说了总之就是找规律,最后用找到的规律对每次输入的n进行类似二进制拆分的处理并统计答案。说是类似是因为它不用真的拆成二进制而是直接按2的次幂一层一层处理下去。这样时间复杂度也是O(logn)的。(和题解一样优秀)至于那个规律,自己写个程序打表来推就行。也可以见代码
代码如下
#include
using namespace std;
int m,T,poi,tot,c,v;
long long int n,nn;
long long int jd[70][70],t[70],p[70],ans;
int main()
{
// freopen("math.in","r",stdin);
// freopen("math.out","w",stdout);
cin>>T;
t[0]=1;
for(int i=1;i<=64;i++)
{
t[i]=t[i-1]*2;
}
p[0]=1;
for(int i=1;i<=63;i++)
{
p[i]=p[i-1]+t[i*2-2];
}
for(int i=0;i<=32;i++)
{
jd[i][i]=t[i*2];
jd[i][i+1]=p[i]+p[i+1];
for(int j=i+2;j<=63;j++)
{
jd[i][j]=jd[i][j-1]*2-p[i];
}
}
// cout<<p[10]<<endl;
// cout<<jd[3][7]<n;
poi=0;
while(n>=t[poi+1])
{
poi++;
}
// cout<<poi<<endl;
ans=p[poi];
n-=t[poi];
if(n==0)
{
v=1;
}
else
{
v=0;
}
// cout<<n=t[poi])
{
// cout<<n<<" "<<t[poi]<<" "<<poi<<" "<<jd[poi][c]<<" "<<jd[poi][c]+p[poi]*((nn+1)/2/t[poi]-1)<<endl;
// cout<< ((nn+1)/t[poi]-1)/2<<" "<<p[poi+1]<<endl;
// cout<<"dw"<<endl;
int f;
f=((nn+1)/t[poi]-1)/2;
if(f<0)
{
f=0;
}
ans+=jd[poi][c]+p[poi+1]*f;
//-------------------------------50pts
ans%=998244353;
//只有50分?
//取模好玩
//玩取模玩的
//---------------------------------50pts
n-=t[poi];
}
poi--;
// c--;
}
/* if(v==0&&n%2==0)
{
ans--;
}*/
cout<<ans%998244353<<endl;
}
}
然后重头戏:
做系统的经历——–>
前面没什么好说的,win10 x64的ghost包我一直存在硬盘里(虽然在今天之前一次也没用过,倒是win7 的包用了好几次)直到今天才用上。然后就是常规的进PE,检查硬盘,备份,然后开始解压镜像。(ASUS的笔记本进bios的键位真是奇葩,一般电脑都是delete,F8之类的,这台电脑却是ESC和F2组合。我试了半天,鬼知道进到了原来的win7系统多少次才成功进bios更改启动首选项并成功进入PE系统。)然后在去聚餐前解压完成了,进入win10 ghost的自动安装界面。然后就快乐地(?)去聚餐了
这是ghost自带的自动安装程序的界面
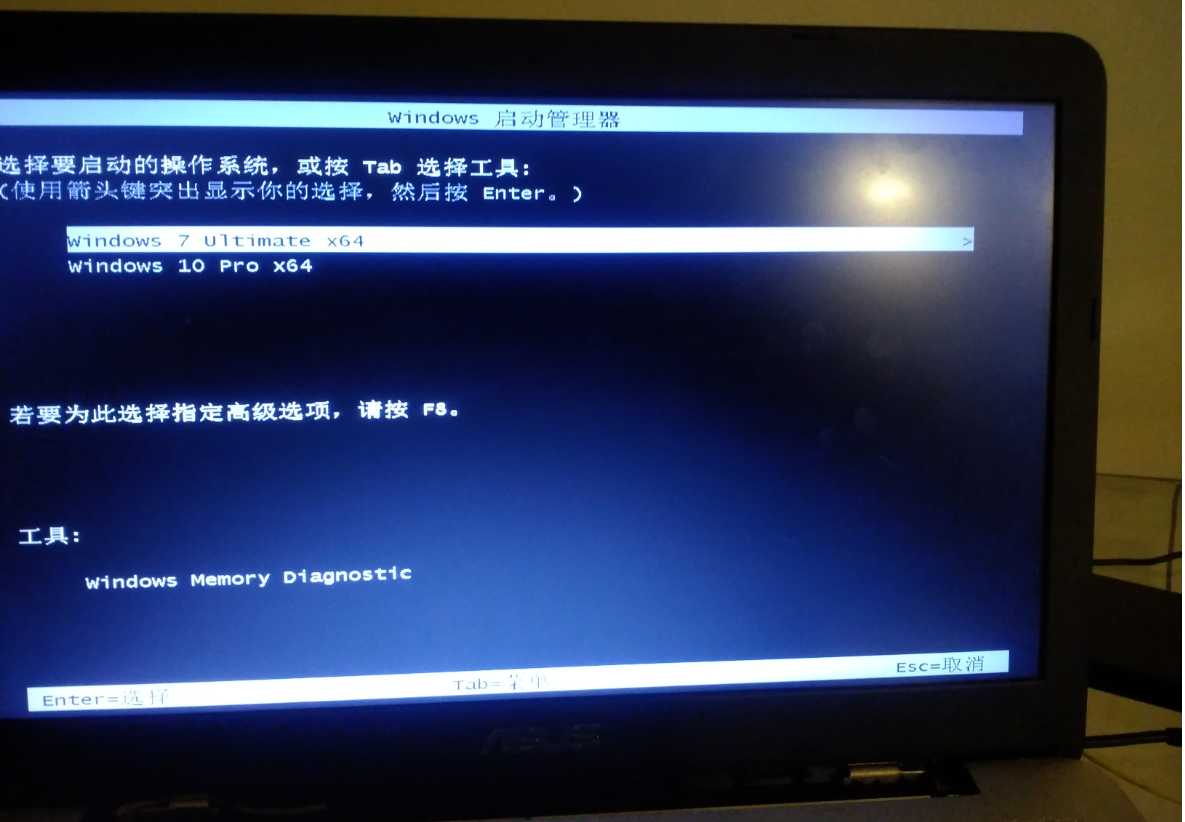
吃完饭回来已经进系统了。但这还没完。因为我保留了win7系统,也就是说,我是在装双系统。但是由于一些特性,PE系统在安装win10的时候把系统启动引导,也就是mbr分区里面的东西删掉了,然后写入了win10的引导。那么win7的引导不就挂了吗?这也就是说,现在只能进win10系统,win7系统虽然还在,但是无法启动,因为没有引导。这怎么办呢?只能再进一次PE进行引导修复了。(又在进PE这里卡了很久,这次记得快捷键了,但忘了我的PE系统U盘的名字,所以改了好几次启动首选项,进了好几次win10)。进去PE后又是常规的引导修复,到这里,win7和win10的引导都被载入mbr分区了。那么在启动时就能手动选择系统。
这就是mbr分区有两个引导时启动时的界面
然后到这里双系统算是装好了.
这就是装好的win10的界面
这就完了?理论上应该是这样,但是我电脑的独立显卡又给我搞了一堆麻烦。事情是这样的:我打开任务管理器的性能时,发现我显卡那里只有一个HD 520(cpu是6代i5)。我TM辣么大一个独显呢?到这里,可以直接判断独显的驱动并没打上了。一扫描,果然。
如图,英伟达920M独显的驱动爆红

本来这也简单,去官网下一个就完了,然而不知道是版本过新还是咋样,官网的驱动与我的系统不兼容。这下问题就大条了。后来试了好几个版本的驱动都不行。
官网的驱动会在安装过程中炸掉.emmmm,爆炸现场忘记截图了
最后,在360驱动大师的帮助下成功装上了。360驱动大师可能是360全家桶里唯一有点用的东西了。
就这么搞定了

大概就这样了,完结撒花(其实是YY来了)
