又又寄了,梅开三度
T1 赛时没能搞定,最后一步炸了。题解是logn的,但数据只有1e7,所以我用的o(n)算法在理论上时间复杂度也是对的(o(q)查询。讲题解就没意思了,在blog就要讨论自己的思路。首先打表找规律。发现对于从a1到ai的子集最大和sumi有:sum[i]=sum[i-1]+sum[lst[i]]-sum[lst[i]-1].其中lst[i]表示ai-1到a1中第一个小于ai的数。(至于这个lst数组,可以跑一遍for循环用栈在O(n)内处理出来。具体来说就是对于每一个数若比栈顶元素大就开始让栈顶元素出栈直到栈顶元素小于当前扫描到的值,然后该值入栈。)
如图(手玩样例)
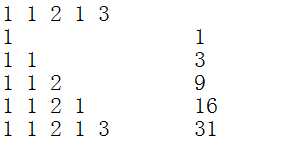
但是这还不够。这样只能处理l=1的情况。然而显然题目中l!=1。所以现在开始考虑在l!=1时如何求解。
如图,可以轻松(?)看出对于一个区间[1,n]的子集最大和是由三部分构成的。

其一是区间[1,l-1],其二是区间[l,r],其三是区间[r+1,n],而答案所需求的是区间二。在上一步中我们已经求出了整个区间[1,n]的子集和,那么显然所求答案就是这个总和减去区间一和区间三的子集和。既然这样对于该问题我们只需求出区间一和区间三便可得到答案(其实没那么简单,两个区间直接减的话会出现重叠部分,使答案偏小。这个下面在谈)在图一中,我们求出了区间[1,i]的子集和,那么区间一就出来了。区间三可以参考区间一的求法,把序列翻转后重复操作即可。如果还不能理解直接上图。
如图,真的只是把图一的步骤倒过来跑一遍
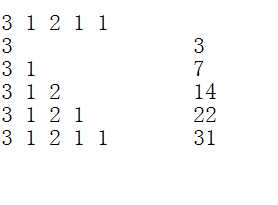
然后将总的子集和减去这两个区间就完(W)事(A)了。在样例中有一个点(输入 2 4 输出 7 答案 10)比输出小了3。仔细研究可以发现删去区间一后对区间二的值会产生影响。
直接上图,可以发现删去首位3后区间[4,5]的子集和会发生改变。这就是重叠的部分。

问题找到了就好办了。直接在答案加上这两个子集重叠部分(O(n)预处理出来,不然会TLE)就对了。然后这题也大概就是这样了。比题解慢,但好想好打而且复杂度稳定。
本来今天的主题是树链剖分的,然而博客已经超长了
如图,截至上一句话的字数统计
树剖就只能略过了。(反正我自己也没完全搞定)。总之就是一个dfs,线段树,DP,LCA,链式前向星等一大堆东西结合起来的逆天超长还容易爆的算法。