2024年8月18日 – 泉州一中信息学Blog

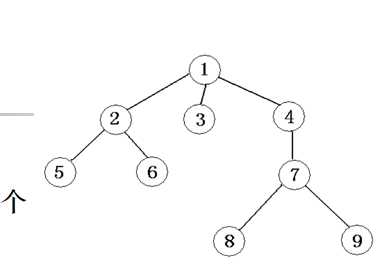
1.树和二叉树

就是一个树状结构，
如下图：

每个元素称为结点（Node）；
有一个特定的结点，称为根结点或树根（Root）；
除根结点外，其余结点被分成m（m≥0）个互不相交的有限集合T1，T2，T3，……，Tm，而每一个子集Ti又都是一棵树，称为原树的子树（Subtree）。
结点的度：有多少个子节点
度为0的是叶子节点
树的深度:树内各节点的度的最大值
先序遍历：根左右上图的先序是：125634789
后序遍历：左右根上图的后序是：562389741
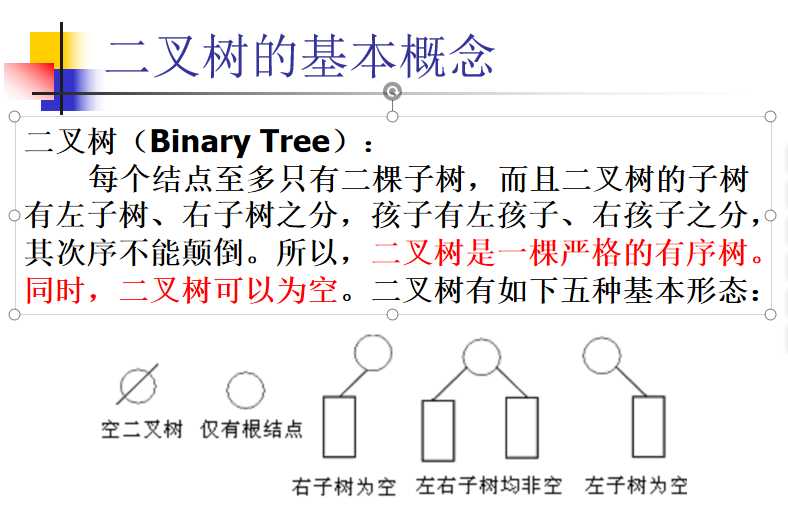
注：二叉树有中序遍历：左根右
满二叉树的一个特殊：
如果有个节点为i(有父节点)
那它的父节点为i/2
它的左孩子是2i,右孩子是2i+1
完全二叉树
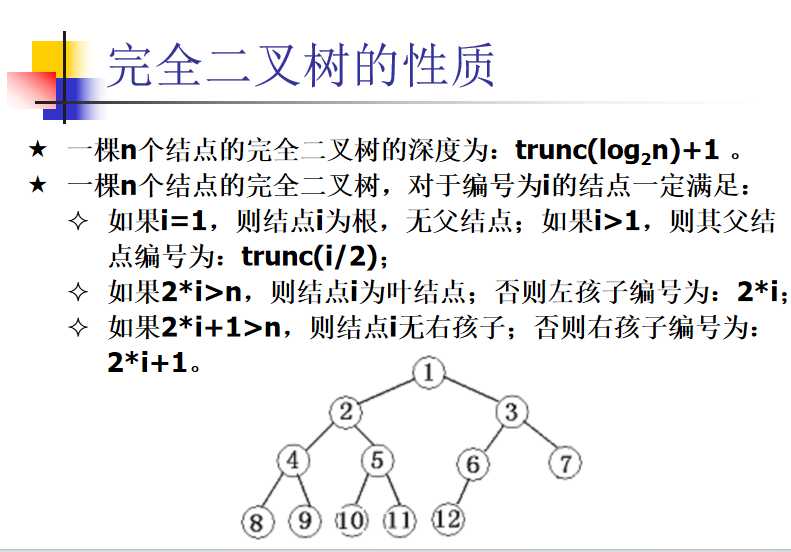
哈夫曼编码
边权上的0代表右节点，1是左节点
并且树是按出现频率排序的

2.优先队列以及大根堆小根堆

定义：
1.priority_queue q；//默认大根堆
2.priority_queue<int,vector,greather> q;//小根堆
操作（和队列基本一样，不重复了

在二叉堆(以小根堆为例)里的两个基本操作：
Put操作：往堆尾加入一个元素，并通过从下往上的调整法，使其继续保持堆的性质；
Get操作：从堆中取出堆头元素，并删除该结点(堆尾覆盖)，再通过从上往下的调整法，使其继续保持堆的性质；

例题1：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
priority_queue<ll,vector<ll>,greater<ll> > q;
ll n,sum,k,x;
int main()
{
    freopen("ugly.in","r",stdin);
    freopen("ugly.out","w",stdout);
    cin>>n;
    q.push(1);
    sum=1;
    while(sum<=n)
    {
        k=q.top();
        //cout<<sum<<" "<<q.top()<<endl;
        q.pop();
        if(x==k) continue;
        sum++;
        q.push(k*2);
        q.push(k*3);
        q.push(k*5);
        q.push(k*7);
        x=k;
    }
    cout<<k;
    return 0;
}

例题2：合并果子
2501 OJ：P369
闲来无事，打了两个代码

#include<bits/stdc++.h>//小根堆 
using namespace std;
#define int long long 
priority_queue<int,vector<int>,greater<int> > q;
int n,a,tot;
signed main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a,q.push(a);
    while(q.size()>1)
    {
        int x=q.top();
        q.pop();
        int y=q.top();
        q.pop();
        q.push(x+y);
        tot+=x+y;
    }
    cout<<tot;
    return 0;
}

#include<bits/stdc++.h>//大根堆 
using namespace std;
int n,x,sum,y;
priority_queue<int> q;
int main()
{
    freopen("fruit.in","r",stdin);
    freopen("fruit.out","w",stdout);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>x;
        q.push(-x);
    }
    while(q.size()-1>0)
    {
        x=-q.top();
        q.pop();
        y=-q.top();
        q.pop();
        q.push(-x-y);
    //  cout<<x<<" "<<y<<endl;
        sum+=x+y;
    }
    cout<<sum<<endl;
    return 0;
}

二叉查找树
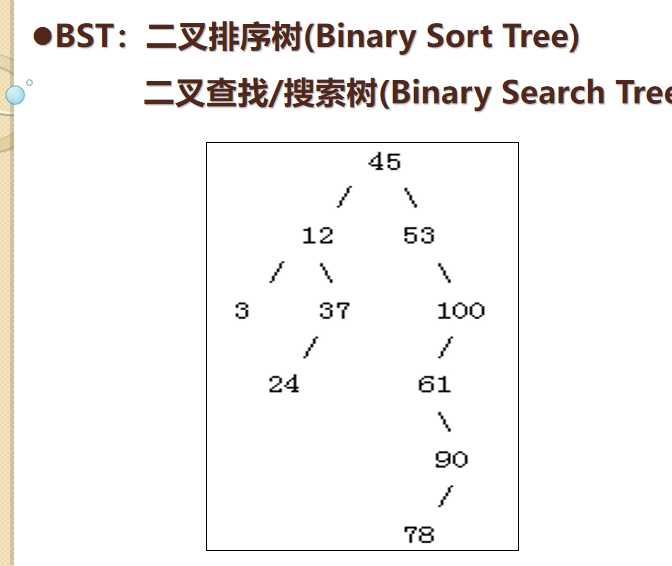
BST定义：
二叉排序树或者是空树或者是满足如下性质的二叉树：
①若它的左子树非空，则左子树上所有结点的值均小于根结点的值；
②若它的右子树非空，则右子树上所有结点的值均大于根结点的值；
③左、右子树本身又各是一棵二叉排序树。
最后它将进化为平衡树（

3.并查集

这是一个很古老的东西，毕竟这以及是我今天第三次学了
这个我还是掌握的不错的
就是写两个函数：一个是合并，一个是查找
也没有什么可以解释：
直接上代码：

int find(int x)
{
    if(fr[x]==x) return x;
    return fr[x]=find(fr[x]);
}
void hebing(int c,int d)
{
    fr[find(c)]=find(d);
}

1.亲戚

很早以前打过了，再打一遍
题目见：2501 OJ P346

#include<bits/stdc++.h>
using namespace std;
int m,n,q,a,b,c,d,xa,xb; 
int fa[20005];
int find(int x)
{
    if(x==fa[x]) return x;
    return fa[x]=find(fa[x]);
}
void hebing(int x,int y)
{
    fa[xa]=xb;
}
int main()
{
    freopen("relation.in","r",stdin);
    freopen("relation.out","w",stdout);
    cin>>n>>m;
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        scanf("%d%d",&a,&b);
        xa=find(a);
        xb=find(b);
        if(xa!=xb) hebing(a,b);
    }
    cin>>q;
    for(int i=1;i<=q;i++)
    {
        scanf("%d%d",&c,&d);
        if(find(c)!=find(d)) printf("No\n");
        else printf("Yes\n");
    } 
    return 0;
}

2.团伙（2501：P385）

林老师发的PPT的团伙有点不一样

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,fr[1005],b[1005][1005];
char a;
int find(int x)
{
    if(fr[x]==x) return x;
    return fr[x]=find(fr[x]);
}
void hebing(int c,int d)
{
    fr[find(c)]=find(d);
}
int main()
{
    freopen("group.in","r",stdin);
    freopen("group.out","w",stdout);
    cin>>n>>m;
    for(int i=1;i<=n;i++) fr[i]=i; 
    for(int i=1;i<=m;i++)
    {
        cin>>a>>x>>y;
        if(a==&#039;F&#039;) hebing(x,y);
        if(a==&#039;E&#039;)
        {
            b[x][y]=b[y][x]=1;
            for(int j=1;j<=n;j++)
            {
                if(b[y][j]==1) hebing(x,j);
                else if(b[x][j]==1) hebing(y,j);
            }
        }
    }
    int sum=0;
    for(int i=1;i<=n;i++) if(fr[i]==i) sum++;
    cout<<sum;
    return 0;
}

3.家谱（P388）

#include<bits/stdc++.h>
using namespace std;
map<string,string> q;
string s,s1;
char a;
string find(string x)
{
    if(q[x]==x) return q[x];
    return q[x]=find(q[x]);
}
int main()
{
    freopen("gen.in","r",stdin);
    freopen("gen.out","w",stdout);
    while(cin>>a && a!=&#039;$&#039;)
    {
        cin>>s;
        if(a==&#039;#&#039;) 
        {
            s1=s;
            if(q[s]=="") q[s]=s;
        }
        else if(a==&#039;+&#039;) q[s]=s1;
        else if(a==&#039;?&#039;)
            cout<<s<<" "<<find(s)<<endl;
    }
    return 0;
}

4.朋友

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y,fr[30001],fri[30005];
char a;
int find(int x)
{
    if(fr[x]==x) return x;
    return fr[x]=find(fr[x]);
}
void hebing(int c,int d)
{
    fr[find(c)]=find(d);
}
int main()
{
    freopen("friend.in","r",stdin);
    freopen("friend.out","w",stdout);
    cin>>n>>m;
    for(int i=1;i<=n;i++) fr[i]=i; 
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        hebing(x,y);
    }
    int maxn=0;
    for(int i=1;i<=n;i++) fri[find(i)]++;
    for(int i=1;i<=n;i++)
        if(fri[i]>0) maxn=max(maxn,fri[i]);
    cout<<maxn;
    return 0;
}

5.食物链（OJ：390）

这是一道很抽象的题目
很成功的把我自己绕进去了

#include<bits/stdc++.h>
using namespace std;
int k,n,d,x,y; 
int fa[300005];
int find(int xi)
{
    if(xi==fa[xi]) return xi;
    return fa[xi]=find(fa[xi]);
}
void hebing(int xi,int yi)
{
    int xa=find(xi);
    int xb=find(yi); 
    fa[xa]=xb;
}
int main()
{
    //freopen("eat.in","r",stdin);
    //freopen("eat.out","w",stdout);
    cin>>n>>k; 
    for(int i=1;i<=3*n;i++) fa[i]=i;
    //假设 x 为本身，那设 x+n 为猎物，那设 x+2*n为天敌； 
    int sum=0;
    for(int i=1;i<=k;++i)
    {
        cin>>d>>x>>y;
        if(x>n || y>n) {sum++;continue;}
        if(d==1)
        {
            if(find(x+n)==find(y) || find(x+2*n)==find(y)){sum++;continue;}
            //如果x和 y 是猎物或天敌的关系，就是假话；
            hebing(x,y);hebing(x+n,y+n);hebing(x+2*n,y+2*n);
            //如果x和y是同类，合并x和y的同类和猎物和天敌 
        }
        else if(d==2)
        {
            if(x==y) {sum++;continue;}
            if(find(x)==find(y) || find(x+2*n)==find(y)) {sum++;continue;}
            //如果x和y是天敌或着同类,就是假话；
            hebing(x,y+n*2);hebing(x+n,y);hebing(x+2*n,y+n);
            //如果y是X的猎物，则x的同类是 y的天敌，x的猎物是y的同类，x的天敌是y的猎物 
        }
    }
    cout<<sum; 
    return 0;
}

一	二	三	四	五	六	日
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

每日归档： 2024年8月18日

常州Day7

常州day7

2024常州day7

1.树和二叉树

2.优先队列以及大根堆小根堆

例题1：

3.并查集

1.亲戚

2.团伙（2501：P385）

3.家谱（P388）

4.朋友

5.食物链（OJ：390）

2024 CZYZ DAY7

常州集训Day7

常州暑假集训Day7

常州Seven Day堆，二叉树

2024常州暑假集训Day7——8.18

24常州集训Day7

常州集训Day7——8.18